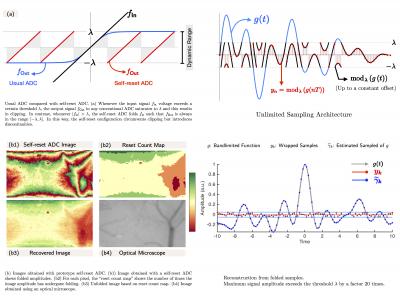
In a recent paper [1], we introduced the concept of “Unlimited Sampling”. This unique approach circumvents the clipping or saturation problem in conventional analog-to-digital converters (ADCs) by considering a radically different ADC architecture which resets the input voltage before saturation. Such ADCs, also known as Self-Reset ADCs (SR-ADCs), allow for sensing modulo samples. In analogy to Shannon’s sampling theorem, the unlimited sampling theorem proves that a bandlimited signal can be recovered from modulo samples provided that a certain sampling density criterion, that is independent of the ADC threshold, is satisfied. In this way, our result allows for perfect recovery of a bandlimited function whose amplitude exceeds the ADC threshold by orders of magnitude. By capitalizing on this result, in this paper, we consider the inverse problem of recovering a sparse signal from its low-pass filtered version. This problem frequently arises in several areas of science and engineering and in context of signal processing, it is studied in several flavors, namely, sparse or FRI sampling, super-resolution and sparse deconvolution. By considering the SR-ADC architecture, we develop a sampling theory for modulo sampling of low-pass filtered spikes. Our main result consists of a new sparse sampling theorem and an algorithm which stably recovers a K–sparse signal from low-pass, modulo samples. We validate our results using numerical experiments.