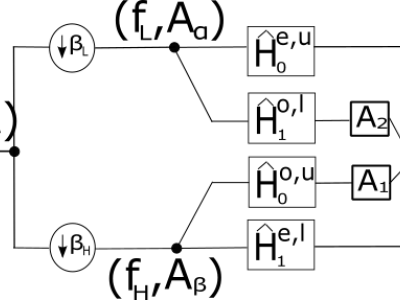
The work by Narang and Ortega (2012, 2013) laid the foundations for the two-channel critically sampled perfect reconstruction
filter bank for signals defined on undirected graphs. The basic filter bank proposed is applicable only to bipartite graphs but using the notion of separable filtering, the basic filter bank can be applied to any arbitrary undirected graphs. In this work several new theoretical results are presented.
In particular, the proposed polyphase analysis yields filtering
structures in the downsampled domain that is equivalent to those before downsampling and
thus can be exploited for efficient implementation. These theoretical results also provide
new insights that can be exploited in the design of these systems. These insights allow
us to generalize these filter banks to directed graphs and to using a variety of
graph base matrices, while also providing a link to the DSP_G framework of Sandryhaila and Moura (2013, 2014). Experiments show evidence that better non-linear approximation results may be obtained by a better select of these base matrices.