
- Read more about A Learning Approach for Wavelet Design
- Log in to post comments
Wavelet analysis and perfect reconstruction filterbanks (PRFBs) are closely related. Desired properties on the wavelet could be translated to equivalent properties on a PRFB. We propose a new learning-based approach towards designing compactly supported orthonormal wavelets with a specified number of vanishing moments. We view PRFBs as a special class of convolutional autoencoders, which places the problem of wavelet/PRFB design within a learning framework. One could then deploy several state-of-the-art deep learning tools to solve the design problem.
- Categories:
 28 Views
28 Views
- Categories:
 40 Views
40 Views
- Read more about STATISTICAL LEARNING OF RATIONAL WAVELET TRANSFORM FOR NATURAL IMAGES
- Log in to post comments
Motivated with the concept of transform learning and the utility of rational wavelet transform in audio and speech processing, this paper proposes Rational Wavelet Transform Learning in Statistical sense (RWLS) for natural images. The proposed RWLS design is carried out via lifting framework and is shown to have a closed form solution. The efficacy of the learned transform is demonstrated in the application of compressed sensing (CS) based reconstruction. The learned RWLS is observed to perform better than the existing standard dyadic wavelet transforms.
- Categories:
 22 Views
22 Views- Read more about DIRECTIONAL DISCRETE COSINE TRANSFORMS ARISING FROM DISCRETE COSINE AND SINE TRANSFORMS FOR DIRECTIONAL BLOCK-WISE IMAGE REPRESENTATION
- Log in to post comments
Directional block transforms (DBTs), such as discrete Fourier transforms, are basically less efficient for sparse image representation
than directional overlapped transforms, such as curvelet and contourlet, but have advantages in practical computation, such as less computational cost, less amount of memory usage to be used, and parallel processing. In order to realize efficient DBTs, this paper proposes
- Categories:
 27 Views
27 Views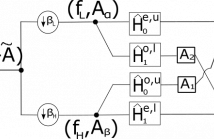
- Read more about Bipartite Graph Filter Banks: Polyphase Analysis and Generalization
- Log in to post comments
The work by Narang and Ortega (2012, 2013) laid the foundations for the two-channel critically sampled perfect reconstruction
filter bank for signals defined on undirected graphs. The basic filter bank proposed is applicable only to bipartite graphs but using the notion of separable filtering, the basic filter bank can be applied to any arbitrary undirected graphs. In this work several new theoretical results are presented.
In particular, the proposed polyphase analysis yields filtering
- Categories:
 23 Views
23 Views
- Read more about Graph Filter Banks With M-Channels, Maximal Decimation, and Perfect Reconstruction
- Log in to post comments
Signal processing on graphs finds applications in many areas. Motivated by recent developments, this paper studies the concept of spectrum folding (aliasing) for graph signals under the downsample-then-upsample operation. In this development, we use a special eigenvector structure that is unique to the adjacency matrix of M-block cyclic matrices. We then introduce M-channel maximally decimated filter banks. Manipulating the characteristics of the aliasing effect, we construct polynomial filter banks with perfect reconstruction property.
- Categories:
 44 Views
44 Views- Read more about Recursive versions of the Levenberg-Marquardt reassigned spectrogram and of the synchrosqueezed
- Log in to post comments
- Categories:
 12 Views
12 Views
- Read more about Low-Complexity Digital Correction of 4-Channel Time-Interleaved ADC Frequency Response Mismatch using Adaptive I/Q Signal Processing
- Log in to post comments
Low-Complexity Digital Correction of 4-Channel Time-Interleaved ADC Frequency Response Mismatch using Adaptive I/Q Signal Processing
- Categories:
 17 Views
17 Views