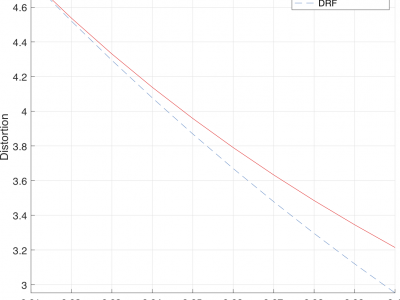
In this paper, we consider the rate-distortion problem where a source X is encoded into k parallel descriptions Y1, . . . , Yk, such that the error signals X - Yi, i = 1, . . . , k, are mutually independent given X. We show that if X is one-sided exponentially distributed, the optimal decoder (estimator) under the one-sided absolute error criterion, is simply given by the maximum of the outputs Y1, . . . , Yk. We provide a closed-form expression for the rate and distortion for any k number of parallel descriptions and for any coding rate. We furthermore show that as the coding rate per description becomes asymptotically small, encoding into k parallel descriptions and using the maximum output as the source estimate, is rate-distortion optimal.