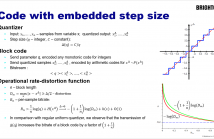
- Read more about Block Codes with Embedded Quantization Step Size Information
- Log in to post comments
If we quantize a block of n samples and then transmit information about quantization step size in the same bitstream, we may naturally expect such a code to be at least O(1/n) redundant. However, as we will show in this paper, this may not necessarily be true. Moreover, we prove that asymptotically, such codes can be as efficient as block codes without embedded step-size information. The proof relies on results from the Diophantine approximations theory. We discuss the significance of this finding for practical applications, such as the design of audio and video coding algorithms.
- Categories:
 104 Views
104 Views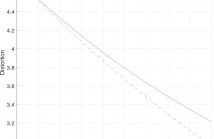
- Read more about The Exponential Distribution in Rate Distortion Theory: The Case of Compression with Independent Encodings
- Log in to post comments
In this paper, we consider the rate-distortion problem where a source X is encoded into k parallel descriptions Y1, . . . , Yk, such that the error signals X - Yi, i = 1, . . . , k, are mutually independent given X. We show that if X is one-sided exponentially distributed, the optimal decoder (estimator) under the one-sided absolute error criterion, is simply given by the maximum of the outputs Y1, . . . , Yk. We provide a closed-form expression for the rate and distortion for any k number of parallel descriptions and for any coding rate.
- Categories:
 95 Views
95 Views