Documents
Presentation Slides
Improved Subspace K-Means Performance via a Randomized Matrix Decomposition
- Citation Author(s):
- Submitted by:
- Trevor Vannoy
- Last updated:
- 14 November 2019 - 7:39pm
- Document Type:
- Presentation Slides
- Document Year:
- 2019
- Event:
- Presenters:
- Trevor Vannoy
- Categories:
- Log in to post comments
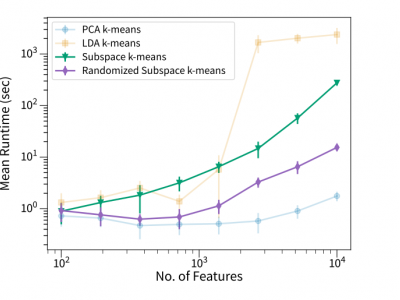
Subspace clustering algorithms provide the capability
to project a dataset onto bases that facilitate clustering.
Proposed in 2017, the subspace k-means algorithm simultaneously
performs clustering and dimensionality reduction with the goal
of finding the optimal subspace for the cluster structure; this
is accomplished by incorporating a trade-off between cluster
and noise subspaces in the objective function. In this study,
we improve subspace k-means by estimating a critical transformation
matrix via a randomized eigenvalue decomposition.
Our modification results in an order of magnitude runtime
improvement on high dimensional data, while retaining the
simplicity, interpretable subspace projections, and convergence
guarantees of the original algorithm.

