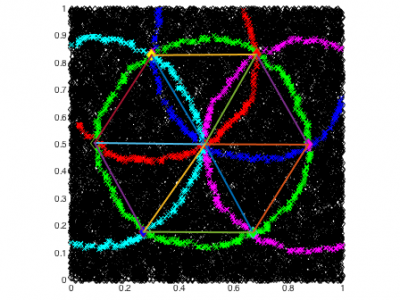
We consider the problem of determining the Euclidean embedding of a dense, planar sensor network. The sensors are equipped with a binary sensing protocol that enables them to detect the neighboring sensors within a fixed radius, R. Using only this connectivity graph, we reconstruct an approximate embedding of the network on an Euclidean plane. To that end, we design an algorithm to identify special landmark nodes in the network whose Euclidean embedding is ``close'' to the vertices of an ideal hexagonal lattice. We present theoretical bounds on the error between this reconstructed embedding of the lattice and its actual embedding. We also provide validation of our algorithm and theoretical results via simulation.