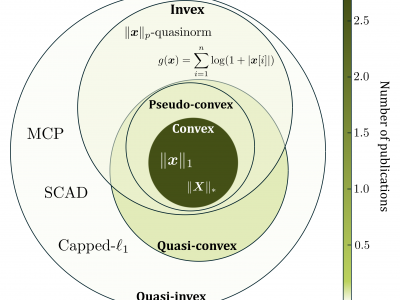
The Alternating Direction Method of Multipliers (ADMM) is uniquely suited for large-scale signal restoration problems, owing to its parallelizability. ADMM has been successfully deployed into several imaging modalities, including blind ptychography, phase retrieval, computer tomography, network unrolling, and magnetic resonance imaging. It is not an overstatement to say that while global convergence guarantees of ADMM under convex objective losses cement its utility, non-convex objectives offer superior reconstruction quality at the expense of these guarantees. In this paper, we break new ground with the development of invex ADMM which retains global optima guarantees for a novel class of non-convex, invex losses - \textit{an invex function is a mapping where any critical point is a global minimizer}. More specifically, we propose a family of invex losses for which ADMM converges to the global minima, along with their guarantees. Our experimental evaluation and theoretical results shows that the proposed approach is very promising, and can aid in extending existing convergences guarantees of ADMM beyond traditional convex settings.