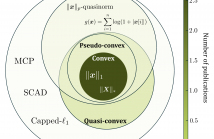
- Read more about Global Convergence of Alternating Direction Method of Multipliers for Invex Objective Losses
- 1 comment
- Log in to post comments
The Alternating Direction Method of Multipliers (ADMM) is uniquely suited for large-scale signal restoration problems, owing to its parallelizability. ADMM has been successfully deployed into several imaging modalities, including blind ptychography, phase retrieval, computer tomography, network unrolling, and magnetic resonance imaging. It is not an overstatement to say that while global convergence guarantees of ADMM under convex objective losses cement its utility, non-convex objectives offer superior reconstruction quality at the expense of these guarantees.
- Categories:
 62 Views
62 Views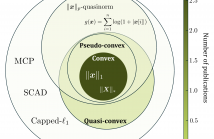
- Read more about Global Convergence of Alternating Direction Method of Multipliers for Invex Objective Losses
- Log in to post comments
The Alternating Direction Method of Multipliers (ADMM) is uniquely suited for large-scale signal restoration problems, owing to its parallelizability. ADMM has been successfully deployed into several imaging modalities, including blind ptychography, phase retrieval, computer tomography, network unrolling, and magnetic resonance imaging. It is not an overstatement to say that while global convergence guarantees of ADMM under convex objective losses cement its utility, non-convex objectives offer superior reconstruction quality at the expense of these guarantees.
- Categories:
 13 Views
13 Views
- Read more about MULTIVARIATE MULTISCALE COSINE SIMILARITY ENTROPY
- Log in to post comments
The rapid development in sensor technology has made it convenient to acquire data from multi-channel systems but has also highlighted the need for the analysis of nonlinear dynamical properties at a higher level - the so-called structural complexity. Traditional single-scale entropy measures, such as the amplitude based Sample Entropy (SampEn), are designed to give a quantification of irregularity and randomness.
- Categories:
 16 Views
16 Views
- Read more about Optimal Measurement Budget Allocation for Particle Filtering
- Log in to post comments
Particle filtering is a powerful tool for target tracking. When the budget for observations is restricted, it is necessary to reduce the measurements to a limited amount of samples carefully selected. A discrete stochastic nonlinear dynamical system is studied over a finite time horizon. The problem of selecting the optimal measurement times for particle filtering is formalized as a combinatorial optimization problem. We propose an approximated solution based on the nesting of a genetic algorithm, a Monte Carlo algorithm and a particle filter.
- Categories:
 26 Views
26 Views
- Read more about Clock synchronization over networks using sawtooth models - Presentation
- Log in to post comments
Clock synchronization and ranging over a wireless network with low communication overhead is a challenging goal with tremendous impact. In this paper, we study the use of time-to-digital converters in wireless sensors, which provides clock synchronization and ranging at negligible communication overhead through a sawtooth signal model for round trip times between two nodes.
- Categories:
 14 Views
14 Views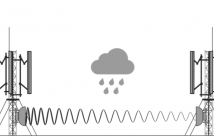
- Read more about Statistical Signal Processing Approach For Rain Estimation Based on Measurements From Network Management Systems
- Log in to post comments
In this talk we present statistical signal processing methodologies on a real-world application of using Commercial Microwave Links (CMLs) as opportunistic sensors for rain monitoring. We formulate an appropriate parameter estimation problem, taking advantage on the empirically evaluated statistics of the rain, and present a new methodology for rain estimation given only the quantized minimum and maximum radio signal level measurements, which are being logged regularly by the network management systems.
- Categories:
 15 Views
15 Views
- Read more about An Iterative Time Domain Denoising Method
- Log in to post comments
This paper focuses on the classical additive noise signal restoration problem. The proposed time domain denoising method iteratively removes outliers. The proposed denoising filter incorporates a threshold operation to determine which sample values are outliers. This method is compared with wavelet soft/hard thresholding and empirical mode decomposition interval thresholding. The proposed method is shown to be a promising method to denoise signals where a frequency decomposition may not be a robust representation of the noise free signal.
- Categories:
 23 Views
23 Views
- Read more about Solving Complex Quadratic Equations with Full-rank Random Gaussian Matrices
- Log in to post comments
We tackle the problem of recovering a complex signal $\mathbf{x}\in\mathbb{C}^n$ from quadratic measurements of the form $y_i=\mathbf{x}^*\mathbf{A}_i\mathbf{x}$, where $\{\mathbf{A}_i\}_{i=1}^m$ is a set of complex iid standard Gaussian matrices. This non-convex problem is related to the well understood phase retrieval problem where $\mathbf{A}_i$ is a rank-1 positive semidefinite matrix.
- Categories:
 17 Views
17 Views
Sensor selection refers to the problem of intelligently selecting a small subset of a collection of available sensors to reduce the sensing cost while preserving signal acquisition performance. The majority of sensor selection algorithms find the subset of sensors that best recovers an arbitrary signal from a number of linear measurements that is larger than the dimension of the signal.
- Categories:
 4 Views
4 Views
- Read more about IMPROVING MULTIKERNEL ADAPTIVE FILTERING WITH SELECTIVE BIAS
- Log in to post comments
In this paper, we propose a scheme to simplify the selection of kernel adaptive filters in a multikernel structure.
By multiplying the output of each kernel filter by an adaptive biasing factor between zero and one, the degrading effects of poorly adjusted kernel filters can be minimized, increasing the robustness of the multikernel scheme. This approach is able to deal with the lack of the necessary statistical information for an optimal adjustment of the filter and its structure.
- Categories:
 13 Views
13 Views