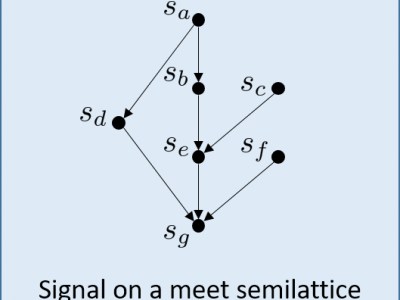
We introduce a novel discrete signal processing framework, called discrete-lattice SP, for signals indexed by a finite lattice. A lattice is a partially ordered set that supports a meet (or join) operation that returns the greatest element below two given elements. Discrete-lattice SP chooses the meet as shift operation and derives associated notion of (meet-invariant) convolution, Fourier transform, frequency response, and a convolution theorem. Examples of lattices include sets of sets that are closed under intersection and trees. Thus our framework is applicable to certain sparse set functions, signals on sparse hypergraphs, and signals on trees. Another view on discrete-lattice SP is as an SP framework for a certain class of directed graphs. However, it is fundamentally different from the prior graph SP as it is based on more than one basic shift and all shifts are always simultaneously diagonalizable.