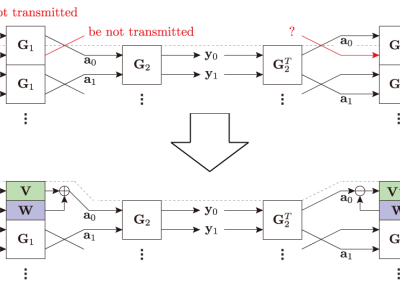
This study presents a pseudo reversible symmetric extension (P-RevSE) that solves the signal boundary problem of lifting-based nonlinear-phase paraunitary filter banks (L-NLPPUFBs), which have high compression rates thanks to their not having a constraint on the linear-phase property unlike the existing transforms used in image coding standards. The conventional L-NLPPUFBs with a periodic extension (PE) yield annoying artifacts at the signal boundaries. However, the P-RevSE is implemented smoothly at the signal boundaries by using a nonexpansive convolution of a symmetric extension (SE) and determinant control for the lifting factorization. Although the determinant control causes a pseudo SE, not a true SE, the resulting L-NLPPUFB with P-RevSE outperforms not only the L-NLPPUFB with PE but also the current transform used in JPEG XR.