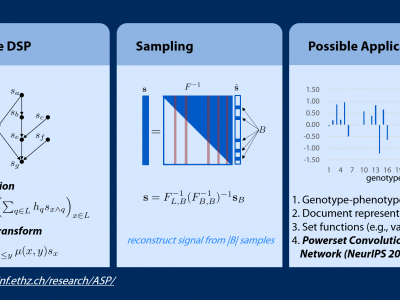
We present a novel sampling theorem, and prototypical applications, for Fourier-sparse lattice signals, i.e., data indexed by a finite semi-lattice. A semilattice is a partially ordered set endowed with a meet (or join) operation that returns the greatest lower bound (smallest upper bound) of two elements. Semilattices can be viewed as a special class of directed graphs with a strictly triangular adjacency matrix , which thus cannot be diagonalized. Our work does not build on prior graph signal processing (GSP) frameworks but on the recently introduced discrete-lattice signal processing (DLSP), which uses the meet as shift operator to derive convolution and Fourier transform. DLSP is fundamentally different from GSP in that it requires several generating shifts that capture the partial-order-rather than the adjacency-structure, and a diagonalizing Fourier transform is always guaranteed by algebraic lattice theory. We apply and demonstrate the utility of our novel sampling scheme in three real-world settings from computational biology, document representation, and auction design.