Documents
Presentation Slides
Presentation Slides
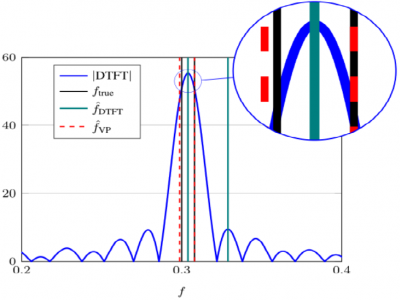
Variable Projection for Multiple Frequency Estimation
- Citation Author(s):
- Submitted by:
- Péter Kovács
- Last updated:
- 6 May 2020 - 3:40pm
- Document Type:
- Presentation Slides
- Document Year:
- 2020
- Event:
- Presenters:
- Yuneisy E. Garcia Guzman
- Paper Code:
- 3974
- Categories:
- Log in to post comments
The estimation of the frequencies of multiple complex sinusoids in the presence of noise is required in many applications such as sonar, speech processing, communications, and power systems. This problem can be reformulated as a separable nonlinear least squares problem (SNLLS). In this paper, such formulation is derived and a variable projection (VP) optimization is proposed for solving the SNLLS problem and estimate the frequency parameters. We also apply a lethargy type theorem for quantifying the difficulty of the optimization. Moreover, an alternative procedure that speeds up the computation of the exact gradient is presented. Simulation results reveal that the proposed algorithm outperforms existing methods in terms of the MSE.

