Sorry, you need to enable JavaScript to visit this website.

Underwater monitoring and exploration have enhanced significantly due to the wide adoption of Internet of Underwater Things (IoUT). However, IoUT implementation is limited by batteries that require frequent replacement, which is costly and unfeasible due to the hostile aquatic environment. Therefore, it is crucial to implement an energy-efficient solution that maximizes the lifetime of IoUT devices, and hence reduce the overall cost of the system.

Underwater monitoring and exploration have enhanced significantly due to the wide adoption of Internet of Underwater Things (IoUT). However, IoUT implementation is limited by batteries that require frequent replacement, which is costly and unfeasible due to the hostile aquatic environment. Therefore, it is crucial to implement an energy-efficient solution that maximizes the lifetime of IoUT devices, and hence reduce the overall cost of the system.

With the integration of communication and computing, it is expected that part of the computing is transferred to the transmitter side. In this paper we address the general problem of Frequency Modulation (FM) for function approximation through a communication channel. We exploit the benefits of the Discrete Cosine Transform (DCT) to approximate the function and design the waveform. In front of other approximation schemes, the DCT uses basis of controlled dynamic, which is a desirable property for a practical implementation.

We describe recursive unique projection-aggregation (RUPA) decoding and iterative unique projection-aggregation (IUPA) decoding of Reed-Muller (RM) codes, which remove non-unique projections from the recursive projection-aggregation (RPA) and iterative projection-aggregation (IPA) algorithms respectively.
We show that these algorithms have competitive error-correcting performance while requiring up to 95% projections less than the baseline RPA algorithm.

Waveform optimization has recently been shown to be a key technique to boost the efficiency and range of far-field wireless power transfer (WPT). Current research has optimized transmit waveform adaptive to channel state information (CSI) and accounting for energy harvester (EH)’s non-linearity but under the assumption of linear high power amplifiers (HPA) at the transmitter. This paper proposes a channel-adaptive waveform design strategy that optimizes the transmitter's input waveform considering both HPA and EH non-linearities.

Turing computability deals with the question of what is theoretically computable on a digital computer, and hence is relevant whenever digital hardware is used. In this paper we study different possibilities to define computable bandlimited signals and systems. We consider a definition that uses finite Shannon sampling series as approximating functions and another that employs computable continuous functions together with an effectively computable time concentration. We discuss the advantages and drawbacks of both definitions and analyze the connections and differences.

We focus on the Multi-Rate Sampling (MRS) Compressed Sensing (CS) scheme, in which several Analog-to-Digital Converters (ADC) sample in parallel at different sub-Nyquist rates. In this paper, we postulate that a good signal recovery requires the measurement matrix rank (MMR) to be as high as possible. We also present an upper-bound for the MMR. Choosing pairwise coprime sampling rates allows to reach this upper-bound.

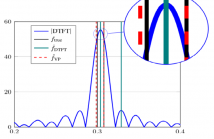
The estimation of the frequencies of multiple complex sinusoids in the presence of noise is required in many applications such as sonar, speech processing, communications, and power systems. This problem can be reformulated as a separable nonlinear least squares problem (SNLLS). In this paper, such formulation is derived and a variable projection (VP) optimization is proposed for solving the SNLLS problem and estimate the frequency parameters. We also apply a lethargy type theorem for quantifying the difficulty of the optimization.