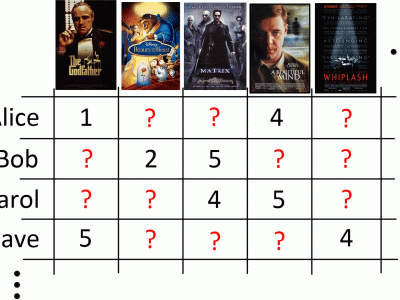
Matrix completion aims to find the missing entries from incomplete observations using the low-rank property. Conventional convex optimization based techniques minimize the nuclear norm subject to a constraint on the Frobenius norm of the residual. However, they are not robust to outliers and have a high computational complexity. Different from the existing schemes based on solving a minimization problem, we formulate matrix completion as a feasibility problem. An alternating projection algorithm is then devised to find a feasible point in the intersection of the low-rank constraint set, and the lp-norm constraint set for handling outlier observations. This presentation is a companion work of: X. Jiang, Z. Zhong, X. Liu and H. C. So, "Robust matrix completion via alternating projection," IEEE Signal Processing Letters, vol. 24, no. 5, pp. 579-583, May 2017