Documents
Poster
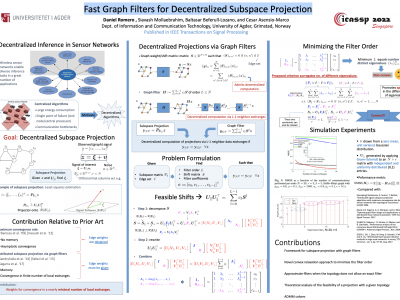
Fast Graph Filters for Decentralized Subspace Projection
- Citation Author(s):
- Submitted by:
- Daniel Romero
- Last updated:
- 6 May 2022 - 4:10pm
- Document Type:
- Poster
- Document Year:
- 2022
- Event:
- Presenters:
- Daniel Romero
- Paper Code:
- SPTM-14.4
- Categories:
- Keywords:
- Log in to post comments
A number of inference problems with sensor networks involve projecting a
measured signal onto a given subspace. In existing decentralized
approaches, sensors communicate with their local neighbors to obtain a
sequence of iterates that asymptotically converges to the desired
projection. In contrast, the present paper develops methods that
produce these projections in a finite and approximately minimal number
of iterations. Building upon tools from graph signal processing, the
problem is cast as the design of a graph filter which, in turn, is
reduced to the design of a suitable graph shift operator. Exploiting
the eigenstructure of the projection and shift matrices leads to an
objective whose minimization yields approximately minimum-order graph
filters. To cope with the fact that this problem is not convex, the
present work introduces a novel convex relaxation of the number of
distinct eigenvalues of a matrix based on the nuclear norm of a
Kronecker difference. To tackle the case where there exists no graph
filter capable of implementing a certain subspace projection with a
given network topology, a second optimization criterion is presented
to approximate the desired projection while trading the number of
iterations for approximation error. Two algorithms are proposed
to optimize the aforementioned criteria based on the
alternating-direction method of multipliers. An exhaustive simulation
study demonstrates that the obtained filters can effectively obtain
subspace projections markedly faster than existing algorithms.

