
- Read more about Truncated Weighted Nuclear Norm Regularization and Sparsity for Image Denoising
- Log in to post comments
The attribute of signal sparsity is widely used to sparse representaion.
The existing nuclear norm minimization and weighted
nuclear norm minimization may achieve a suboptimal in
real application with the inaccurate approximation of rank
function. This paper presents a novel denoising method that
preserves fine structures in the image by imposing L1 norm
constraints on the wavelet transform coefficients and low
rank on high-frequency components of group similar patches.
An efficient proximal operator of Truncated Weighted Nuclear
- Categories:
 18 Views
18 Views
A number of inference problems with sensor networks involve projecting a
measured signal onto a given subspace. In existing decentralized
approaches, sensors communicate with their local neighbors to obtain a
sequence of iterates that asymptotically converges to the desired
projection. In contrast, the present paper develops methods that
produce these projections in a finite and approximately minimal number
of iterations. Building upon tools from graph signal processing, the
problem is cast as the design of a graph filter which, in turn, is
- Categories:
 27 Views
27 Views
Recent work introduced a framework for signal processing (SP) on meet/join lattices. Such a lattice is partially ordered and supports a meet (or join) operation that returns the greatest lower bound and the smallest upper bound of two elements, respectively. Lattices appear in various domains and can be used, for example, to express rankings in social choice theory or multisets in combinatorial auctions. Discrete lattice SP (DLSP) uses the meet operation as shift and derives associated notions of convolution and Fourier transform for signals indexed by lattices.
- Categories:
 9 Views
9 Views
- Read more about Minimax Magnitude Response Approximation of Pole-radius Constrained IIR Digital Filters
- Log in to post comments
Design of infinite impulse response (IIR) digital filters to approximate some desired magnitude-frequency response is a classical research topic in signal processing. When a pole radius constraint is imposed, however, the problem becomes challenging and few solution methods are available. This paper converts the magnitude-response approximation problem into another problem that approximates the desired magnitude response and an accompanied phase response simultaneously.
- Categories:
 16 Views
16 Views
- Categories:
 4 Views
4 Views
- Read more about Bernstein Filter: a new solver for mean curvature regularized models
- Log in to post comments
The mean curvature has been shown a proper regularization in various ill-posed inverse problems in signal processing. Traditional solvers are based on either gradient descent methods or Euler Lagrange Equation. However, it is not clear if this mean curvature regularization term itself is convex or not. In this paper, we first prove that the mean curvature regularization is convex if the dimension of imaging domain is not
- Categories:
 6 Views
6 Views
- Read more about Edge-enhancing filters with negative weights
- Log in to post comments
In [doi{10.1109/ICMEW.2014.6890711}], a~graph-based filtering of noisy images is performed by directly computing a projection of the image to be filtered onto a lower dimensional Krylov subspace of the graph Laplacian, constructed using non-negative graph weights determined by distances between image data corresponding to image pixels. We extend the construction of the graph Laplacian to the case, where some graph weights can be negative.
KGlobalSIP.pdf
- Categories:
 24 Views
24 Views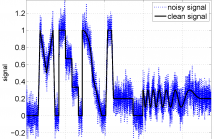
- Read more about Conjugate gradient acceleration of non-linear smoothing filters
- Log in to post comments
The most efficient signal edge-preserving smoothing filters, e.g., for denoising, are non-linear. Thus, their acceleration is challenging and is often done in practice by tuning filters parameters, such as increasing the width of the local smoothing neighborhood, resulting in more aggressive smoothing of a single sweep at the cost of increased edge blurring. We propose an alternative technology, accelerating the original filters without tuning, by running them through a conjugate gradient method, not affecting their quality.
GlobalSIP.pdf
- Categories:
 16 Views
16 Views
Graph-based spectral denoising is a low-pass filtering using the eigendecomposition of the graph Laplacian matrix of a noisy signal. Polynomial filtering avoids costly computation of the eigendecomposition by projections onto suitable Krylov subspaces. Polynomial filters can be based, e.g., on the bilateral and guided filters. We propose constructing accelerated polynomial filters by running flexible Krylov subspace based linear and eigenvalue solvers such as the Block Locally Optimal Preconditioned Conjugate Gradient (LOBPCG) method.
MLSP2015.pdf
- Categories:
 21 Views
21 Views