Documents
Poster
Geometric Invariants for Sparse Unknown View Tomography
- Citation Author(s):
- Submitted by:
- Mona Zehni
- Last updated:
- 11 May 2019 - 7:56pm
- Document Type:
- Poster
- Document Year:
- 2019
- Event:
- Presenters:
- Zhizhen Zhao
- Paper Code:
- 3818
- Categories:
- Keywords:
- Log in to post comments
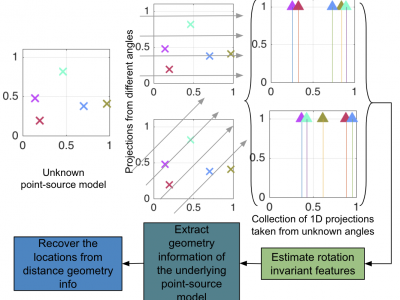
In this paper, we study a 2D tomography problem for point source models with random unknown view angles. Rather than recovering the projection angles, we reconstruct the model through a set of rotation-invariant features that are estimated from the projection data. For a point source model, we show that these features reveal geometric information about the model such as the radial and pairwise distances. This establishes a connection between unknown view tomography and unassigned distance geometry problem (uDGP). We propose new methods to extract the distances and approximate the pairwise distance distribution of the underlying points. We then use the recovered distribution to estimate the locations of the points through constrained non-convex optimization. Our simulation results show that our point source reconstruction pipeline is robust to noise and outperforms the regularized expectation maximization (EM) baseline.

