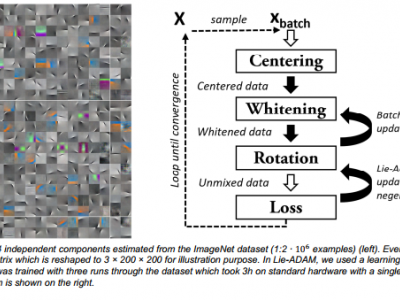
We were interested in computing a mini-batch-capable end-to end algorithm to identify statistically independent components (ICA) in large scale and high-dimensional datasets. Current algorithms typically rely on pre-whitened data and do not integrate the two procedures of whitening and ICA estimation. Our online approach estimates a whitening and a rotation matrix with stochastic gradient descent on centered or uncentered data. We show that this can be done efficiently by combining Batch Karhunen-Löwe-Transformation with Lie group techniques. Our algorithm is recursion-free and can be organized as feed-forward neural network which makes the use of GPU acceleration straight-forward. Because of the very fast convergence of Batch KLT, the gradient descent in the Lie group of orthogonal matrices stabilizes quickly. The optimization is further enhanced by integrating ADAM, an improved stochastic gradient descent (SGD) technique from the field of deep learning. We test the scaling capabilities by computing the independent components of the well-known ImageNet challenge. Due to its robustness with respect to batch and step size, our approach can be used as a drop-in replacement for standard ICA algorithms where memory is a limiting factor.