
- Read more about KLM
- Log in to post comments
Structured Tucker tensor decomposition models complete or incomplete multiway data sets (tensors), where the core tensor and the factor matrices can obey different constraints. The model includes block-term decomposition or canonical polyadic decomposition as special cases. We propose a very flexible optimization method for the structured Tucker decomposition problem, based on the second-order Levenberg-Marquardt optimization, using an approximation of the Hessian matrix by the Krylov subspace method. An algorithm with limited sensitivity of the decomposition is included.
slidy22.pdf
- Categories:
 13 Views
13 Views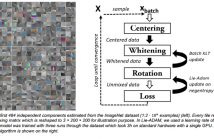
- Read more about LARGE-SCALE INDEPENDENT COMPONENT ANALYSIS BY SPEEDING UP LIE GROUP TECHNIQUES
- Log in to post comments
We were interested in computing a mini-batch-capable end-to end algorithm to identify statistically independent components (ICA) in large scale and high-dimensional datasets. Current algorithms typically rely on pre-whitened data and do not integrate the two procedures of whitening and ICA estimation. Our online approach estimates a whitening and a rotation matrix with stochastic gradient descent on centered or uncentered data. We show that this can be done efficiently by combining Batch Karhunen-Löwe-Transformation with Lie group techniques.
- Categories:
 20 Views
20 Views
- Read more about Independent Vector Analysis using Semi-Parametric Density Estimation via Multivariate Entropy Maximization
- 1 comment
- Log in to post comments
Due to the wide use of multi-sensor technology, analysis of multiple sets of data is at the heart of many challenging engineering problems. Independent vector analysis (IVA), a recent generalization of independent component analysis (ICA), enables the joint analysis of datasets and extraction of latent sources through the use of a simple yet effective generative model. However, the success of IVA is tied to proper estimation of the probability density function (PDF) of the multivariate latent sources; information that is generally unknown.
- Categories:
 95 Views
95 Views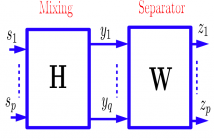
In this article, we propose a Bounded Component Analysis (BCA) approach for the separation of the convolutive mixtures of sparse sources. The corresponding algorithm is derived from a geometric objective function defined over a completely deterministic setting. Therefore, it is applicable to sources which can be independent or dependent in both space and time dimensions. We show that all global optima of the proposed objective are perfect separators. We also provide numerical examples to illustrate the performance of the algorithm.
- Categories:
 31 Views
31 Views- Read more about A PARALLEL CONVOLUTIONAL NEURAL NETWORK ARCHITECTURE FOR STEREO VISION ESTIMATION
- Log in to post comments
ICIP_CNN.pdf
- Categories:
 53 Views
53 Views- Read more about A Parameter-Free Cauchy-Schwartz Information Measure for Independent Component Analysis
- Log in to post comments
Independent component analysis (ICA) by an information measure has seen wide applications in engineering. Different from traditional probability density function based information measures, a probability survival distribution based Cauchy-Schwartz information measure for multiple variables is proposed in this paper. Empirical estimation of survival distribution is parameter-free which is inherited by the estimation of the new information measure.
ica_slide.pdf
- Categories:
 5 Views
5 Views- Read more about Unsupervised Keyword Spotting using Bounded Generalized Gaussian Mixture Model with ICA
- Log in to post comments
In this paper, bounded generalized Gaussian mixture model (BGGMM) using independent component analysis (ICA) is proposed and applied to an existing unsupervised keyword spotting setting for the generation of posteriorgrams. The ICA mixture model is trained without any transcription information to generate the posteriorgrams which further labels the speech frames of the keyword example(s) and test data.
- Categories:
 24 Views
24 Views