In the past two decades convex optimization gained increasing popularity in signal processing and communications, as many fundamental problems in this area can be modelled, analyzed and solved using convex optimization theory and algorithms. In emerging large scale applications such as compressed sensing, massive MIMO and machine learning, the underlying optimization problems often exhibit convexity, however, the classic interior point methods do not scale well with the problem dimensions. Furthermore, in applications that do not exhibit conventional convexity, general purpose gradient methods often show slow convergence.
Recently a variety of iterative descent direction methods gained interest, which can be customized to the requirements of specific applications, accounting for their underlying problem structures and (parallel) hardware architectures. In this tutorial, we capture this trend and address the challenges in designing efficient customized optimization procedures:

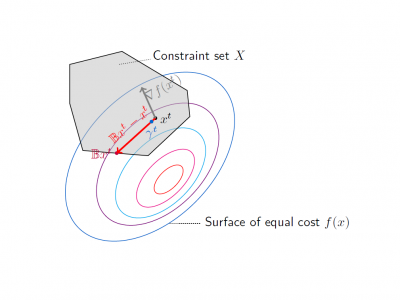
We provide an overview of the state-of-the-art iterative algorithms based on the descent direction procedure, such as the gradient projection method, the Jacobi best-response algorithm, the pricing algorithm, and recent variants that are suitable for parallel and real-time implementation. Furthermore, we introduce a recently developed successive pseudo-convex approximation framework that uses a weaker form of convexity than the conventional convexity. This framework relaxes the traditional convergence conditions, and motivates new algorithms that make better use of the underlying problem structure. Pseudo-convex modelling emerges in numerous problem classes, e.g., the minimization of fractional functions and condition numbers.

We demonstrate the above development by numerous applications including energy efficient networking and sparse signal estimation. Along with these examples we provide guidelines for designing and analyzing new algorithms. The design of customized optimization procedures is rewarding for young researchers in the different application fields. In contrast to the application of general solvers, their use requires creativity and leaves sufficient room for own research contributions. It allows researchers to incorporate their profound knowledge about the application to design efficient customized solutions.