Sorry, you need to enable JavaScript to visit this website.

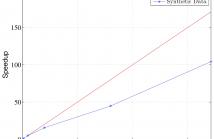
We consider the problem of nonnegative tensor completion. Our aim is to derive an efficient algorithm that is also suitable for parallel implementation. We adopt the alternating optimization framework and solve each nonnegative matrix completion problem via a Nesterov-type algorithm for smooth convex problems. We describe a parallel implementation of the algorithm and measure the attained speedup in a multi-core computing environment. It turns out that the derived algorithm is an efficient candidate for the solution of very large-scale sparse nonnegative tensor completion problems.