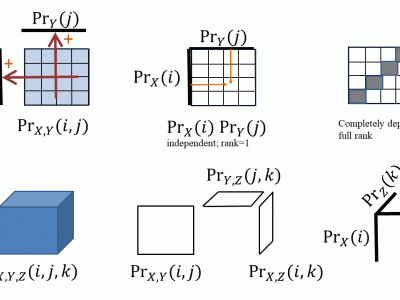
We reveal an interesting link between tensors and multivariate statistics. The rank of a multivariate probability tensor can be interpreted as a nonlinear measure of statistical dependence of the associated random variables. Rank equals one when the random variables are independent, and complete statistical dependence corresponds to full rank; but we show that rank as low as two can already model strong statistical dependence. In practice we usually work with random variables that are neither independent nor fully dependent -- partial dependence is typical, and can be modeled using a low-rank multivariate probability tensor. Directly estimating such a tensor from sample averages is impossible even for as few as ten random variables taking ten values each --yielding a billion unknowns; but we often have enough data to estimate lower-order marginalized distributions. We prove that it is possible to identify the higher-order joint probabilities from lower order ones, provided that the higher-order probability tensor has low-enough rank, i.e., the random variables are only partially dependent. We also provide a computational identification algorithm that is shown to work well on both simulated and real data. The insights and results have numerous applications in estimation, hypothesis testing, completion, machine learning, and system identification. Low-rank tensor modeling thus provides a `universal' non-parametric (model-free) alternative to probabilistic graphical models.