
- Read more about Enhancing GAN Performance through Neural Architecture Search and Tensor Decomposition
- Log in to post comments
Generative Adversarial Networks (GANs) have emerged as a powerful tool for generating high-fidelity content. This paper presents a new training procedure that leverages Neural Architecture Search (NAS) to discover the optimal architecture for image generation while employing the Maximum Mean Discrepancy (MMD) repulsive loss for adversarial training. Moreover, the generator network is compressed using tensor decomposition to reduce its computational footprint and inference time while preserving its generative performance.
- Categories:
 71 Views
71 Views
- Read more about Learning a Low-Rank Feature Representation: Achieving Better Trade-Off Between Stability and Plasticity in Continual Learning
- Log in to post comments
In continual learning, networks confront a trade-off between stability and plasticity when trained on a sequence of tasks. To bolster plasticity without sacrificing stability, we propose a novel training algorithm called LRFR. This approach optimizes network parameters in the null space of the past tasks’ feature representation matrix to guarantee the stability. Concurrently, we judiciously select only a subset of neurons in each layer of the network while training individual tasks to learn the past tasks’ feature representation matrix in low-rank.
LRFR_13Apr.pdf
- Categories:
 30 Views
30 Views
- Read more about The Rao, Wald, and Likelihood-Ratio Tests under Generalized Self-Concordance
- Log in to post comments
Three classical approaches to goodness-of-fit testing are Rao’s test, Wald’s test, and the likelihood-ratio test. The asymptotic equivalence of these three tests under the null hypothesis is a famous connection in statistical detection theory. We revisit these three likelihood-related tests from a non-asymptotic viewpoint under self-concordance assumptions. We recover the equivalence of the three tests and characterize the critical sample size beyond which the equivalence holds asymptotically. We also investigate their behavior under local alternatives.
- Categories:
 22 Views
22 Views
- Read more about Fast Approximation of the Generalized Sliced-Wasserstein Distance
- Log in to post comments
Generalized sliced-Wasserstein distance is a variant of sliced-Wasserstein distance that exploits the power of non-linear projection through a given defining function to better capture the complex structures of probability distributions. Similar to the sliced-Wasserstein distance, generalized sliced-Wasserstein is defined as an expectation over random projections which can be approximated by the Monte Carlo method. However, the complexity of that approximation can be expensive in high-dimensional settings.
- Categories:
 36 Views
36 Views
- Read more about Meta-Learning with Versatile Loss Geometries for Fast Adaptation Using Mirror Descent
- Log in to post comments
Utilizing task-invariant prior knowledge extracted from related tasks, meta-learning is a principled framework that empowers learning a new task especially when data records are limited. A fundamental challenge in meta-learning is how to quickly "adapt" the extracted prior in order to train a task-specific model within a few optimization steps. Existing approaches deal with this challenge using a preconditioner that enhances convergence of the per-task training process.
- Categories:
 57 Views
57 Views
- Read more about Large Dimensional Analysis of LS-SVM Transfer Learning (application on PolSAR)
- Log in to post comments
- Categories:
 15 Views
15 Views
- Read more about Model-Free Learning of Optimal Beamformers for Passive IRS-Assisted Sumrate Maximization
- Log in to post comments
Although Intelligent Reflective Surfaces (IRSs) are a cost-effective technology promising high spectral efficiency in future wireless networks, obtaining optimal IRS beamformers is a challenging problem with several practical limitations. Assuming fully-passive, sensing- free IRS operation, we introduce a new data-driven Zeroth-order Stochastic Gradient Ascent (ZoSGA) algorithm for sumrate optimization in an IRS-aided downlink setting.
ZoSGA_Poster.pdf
- Categories:
 49 Views
49 Views
- Read more about FAST SINGLE-PERSON 2D HUMAN POSE ESTIMATION USING MULTI-TASK CONVOLUTIONAL NEURAL NETWORKS
- Log in to post comments
This paper presents a novel neural module for enhancing existing fast and lightweight 2D human pose estimation CNNs, in order to increase their accuracy. A baseline stem CNN is augmented by a collateral module, which is tasked to encode global spatial and semantic information and provide it to the stem network during inference. The latter one outputs the final 2D human pose estimations.
2023041536.pdf
- Categories:
 17 Views
17 Views
- Read more about Designing Transformer networks for sparse recovery of sequential data using deep unfolding
- Log in to post comments
Deep unfolding models are designed by unrolling an optimization algorithm into a deep learning network. These models have shown faster convergence and higher performance compared to the original optimization algorithms. Additionally, by incorporating domain knowledge from the optimization algorithm, they need much less training data to learn efficient representations. Current deep unfolding networks for sequential sparse recovery consist of recurrent neural networks (RNNs), which leverage the similarity between consecutive signals.
- Categories:
 32 Views
32 Views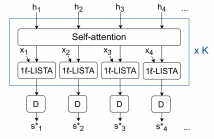
- Read more about Designing Transformer networks for sparse recovery of sequential data using deep unfolding: Presentation
- Log in to post comments
Deep unfolding models are designed by unrolling an optimization algorithm into a deep learning network. These models have shown faster convergence and higher performance compared to the original optimization algorithms. Additionally, by incorporating domain knowledge from the optimization algorithm, they need much less training data to learn efficient representations. Current deep unfolding networks for sequential sparse recovery consist of recurrent neural networks (RNNs), which leverage the similarity between consecutive signals.
- Categories:
 27 Views
27 Views