- Read more about An Efficient Alternative to Network Pruning through Ensemble Learning
- Log in to post comments
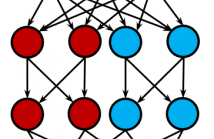
Convolutional Neural Networks (CNNs) currently represent the best tool for classification of image content. CNNs are trained in order to develop generalized expressions in form of unique features to distinguish different classes. During this process, one or more filter weights might develop the same or similar values. In this case, the redundant filters can be pruned without damaging accuracy.Unlike normal pruning methods, we investigate the possibility of replacing a full-sized convolutional neural network with an ensemble of its narrow versions.
- Categories:
 74 Views
74 Views
- Read more about Generic Bounds on the Maximum Deviations in Sequential/Sequence Prediction (and the Implications in Recursive Algorithms and Learning/Generalization)
- Log in to post comments
In this paper, we derive generic bounds on the maximum deviations in prediction errors for sequential prediction via an information-theoretic approach. The fundamental bounds are shown to depend only on the conditional entropy of the data point to be predicted given the previous data points. In the asymptotic case, the bounds are achieved if and only if the prediction error is white and uniformly distributed.
- Categories:
 54 Views
54 Views