
- Read more about Effective Approximation of Bandlimited Signals and Their Samples
- Log in to post comments
- Categories:
 19 Views
19 Views
- Read more about Track-before-detect for sub-Nyquist radar
- Log in to post comments
Sub-Nyquist radars require fewer measurements, facilitating low-cost design, flexible resource allocation, etc. By applying compressed sensing (CS) method, such radars achieve close performance to traditional Nyquist radars. However in low signal-to-noise ratio (SNR) scenarios, detecting weak targets is challenging: low probability of detection and many spurious targets could occur in the recovery results of traditional CS method.
- Categories:
 28 Views
28 Views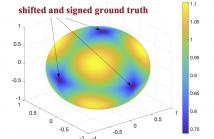
- Read more about MANIFOLD GRADIENT DESCENT SOLVES MULTI-CHANNEL SPARSE BLIND DECONVOLUTION PROVABLY AND EFFICIENTLY
- Log in to post comments
Multi-channel sparse blind deconvolution refers to the problem of learning an unknown filter by observing its circulant convolutions with multiple input signals that are sparse. It is challenging to learn the filter efficiently due to the bilinear structure of the observations with respect to the unknown filter and inputs, leading to global ambiguities of identification. We propose a novel approach based on nonconvex optimization over the sphere manifold by minimizing a smooth surrogate of the sparsity-promoting loss function.
- Categories:
 18 Views
18 Views
- Read more about Scalable trellis quantization for JPEG XS
- Log in to post comments
Trellis quantization as structured vector quantizer is able to improve
the rate-distortion performance of traditional scalar quantizers. As such,
it has found its way into the JPEG~2000 standard, and also recently as an
option in HEVC. In this paper, a trellis quantization option for JPEG XS is
considered and analyzed; JPEG~XS is a low-complexity, low-latency high-speed
"mezzanine" codec for Video over IP transmission in professional
production environments and industrial applications where high compression
- Categories:
 60 Views
60 Views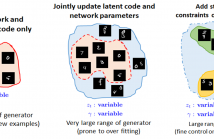
- Read more about GENERATIVE MODELS FOR LOW-RANK VIDEO REPRESENTATION AND RECONSTRUCTION FROM COMPRESSIVE MEASUREMENTS
- Log in to post comments
Generative models have recently received considerable attention in the field of compressive sensing. If an image belongs to the range of a pretrained generative network, we can recover it from its compressive measurements by estimating the underlying compact latent code. In practice, all the pretrained generators have certain range beyond which they fail to generate reliably. Recent researches show that convolutional generative structures are biased to generate natural images.
- Categories:
 36 Views
36 Views
- Read more about Bayesian Design of Sampling Set for Bandlimited Graph Signals
- Log in to post comments
The design of sampling set (DoS) for bandlimited graph signals (GS) has been extensively studied in recent years, but few of them
poster_xx.pdf
- Categories:
 35 Views
35 Views
- Categories:
 44 Views
44 Views
- Read more about One-Bit Unlimited Sampling
- Log in to post comments
Conventional analog–to–digital converters (ADCs) are limited in dynamic range. If a signal exceeds some prefixed threshold, the ADC saturates and the resulting signal is clipped, thus becoming prone to aliasing artifacts. Recent developments in ADC design allow to overcome this limitation: using modulo operation, the so called self-reset ADCs fold amplitudes which exceed the dynamic range. A new (unlimited) sampling theory is currently being developed in the context of this novel class of ADCs.
- Categories:
 82 Views
82 Views
- Read more about The discrete cosine transform on triangles
- Log in to post comments
- Categories:
 13 Views
13 Views
- Read more about Solving Continuous-Domain Inverse Problems Exactly with B-splines
- Log in to post comments
- Categories:
 22 Views
22 Views