
- Read more about Linear Complexity Gibbs Sampling for Generalized Labeled Multi-Bernoulli Filtering
- Log in to post comments
Generalized Labeled Multi-Bernoulli (GLMB) densities arise in a host of multi-object system applications analogous to Gaussians in single-object filtering. However, computing the GLMB filtering density requires solving NP-hard problems. To alleviate this computational bottleneck, we develop a linear complexity Gibbs sampling framework for GLMB density computation.
- Categories:
 15 Views
15 Views
- Read more about Cyclic Misspecified Cramer-Rao Bound for Periodic Parameter Estimation
- Log in to post comments
In many practical parameter estimation problems, the observation model is periodic with respect to the unknown parameters. In these cases, the appropriate estimation criterion is periodic in the parameter space, and cyclic performance bounds should be used. However, existing cyclic performance bounds do not account for the common scenario of model misspecification. The misspecified Cramér-Rao bound (MCRB) provides a lower bound on the mean-squared-error (MSE) for estimation problems under model misspecification. However, the MCRB does not provide a valid bound for periodic problems.
- Categories:
 7 Views
7 Views
- Read more about A graph-prediction-based approach for debiasing underreported data
- Log in to post comments
We present a novel Graph-based debiasing Algorithm for Underreported Data (GRAUD) aiming at an efficient joint estimation of event counts and discovery probabilities across spatial or graphical structures. This innovative method provides a solution to problems seen in fields such as policing data and COVID-19 data analysis. Our approach avoids the need for strong priors typically associated with Bayesian frameworks. By leveraging the graph structures on unknown variables n and p, our method debiases the under-report data and estimates the discovery probability at the same time.
- Categories:
 5 Views
5 Views
- Read more about PENDANTSS: PEnalized Norm-Ratios Disentangling Additive Noise, Trend and Sparse Spikes
- Log in to post comments
Denoising, detrending, deconvolution: usual restoration tasks, traditionally decoupled. Coupled formulations entail complex ill-posed inverse problems. We propose PENDANTSS for joint trend removal and blind deconvolution of sparse peak-like signals. It blends a parsimonious prior with the hypothesis that smooth trend and noise can somewhat be separated by low-pass filtering.
- Categories:
 36 Views
36 Views
- Read more about [Slides] Multi-Sensor Multi-Scan Radar Sensing of Multiple Extended Targets
- Log in to post comments
We propose an efficient solution to the state estimation problem in multi-scan multi-sensor multiple extended target sensing scenarios. We first model the measurement process by a doubly inhomogeneous-generalized shot noise Cox process and then estimate the parameters using a jump Markov chain Monte Carlo sampling technique. The proposed approach scales linearly in the number of measurements and can take spatial properties of the sensors into account, herein, sensor noise covariance, detection probability, and resolution.
- Categories:
 13 Views
13 Views
- Read more about Non-uniform Frequency Spacing for Regularization-free Gridless DOA
- Log in to post comments
Gridless direction-of-arrival (DOA) estimation with multiple frequencies can be applied to acoustic source localization. We formulate this as an atomic norm minimization (ANM) problem and derive a regularization-free semi-definite program (SDP) avoiding regularization bias. We also propose a fast SDP program to deal with non-uniform frequency spacing. The DOA is retrieved via irregular Vandermonde decomposition (IVD), and we theoretically guarantee the existence of the IVD. We extend ANM to the multiple measurement vector setting and derive its equivalent regularization-free SDP.
- Categories:
 9 Views
9 Views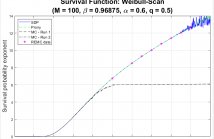
- Read more about New Results on the Weibull Distribution and Weibull Sums, with Application to Radar Sea Clutter
- Log in to post comments
This work covers and combines three themes concerning the Weibull distribution in the heavy-tailed region, as is relevant to sea clutter: (i) Characterizing the Weibull distribution as a compound clutter model and deriving a computationally tractable form for its implied texture distribution. (ii) Computing the distribution of a positively weighted sum of independent identically distributed (iid) Weibull random variables -- facilitated by the compound formulation, with emphasis on the tail.
- Categories:
 20 Views
20 Views
- Read more about Waveform design to improve the estimation of target parameters using the Fourier Transform method in a MIMO OFDM DFRC system
- Log in to post comments
Among the approaches used to jointly estimate the directions of arrival (DOAs) of K targets in a multiple-input multiple-output dual-function radar communication system, the method based on the identification of the K largest local maxima of the modulus of the Fourier transform (FT) of the signal received by the antennas has the advantage of having a low computational cost. However, the local maxima do not necessarily correspond to the values of interest. To avoid this problem, we present an operation mode making it possible to address the estimations of the DOAs separately.
- Categories:
 20 Views
20 Views
- Read more about Waveform design to improve the estimation of target parameters using the Fourier Transform method in a MIMO OFDM DFRC system
- Log in to post comments
Among the approaches used to jointly estimate the directions of arrival (DOAs) of K targets in a multiple-input multiple-output dual-function radar communication system, the method based on the identification of the K largest local maxima of the modulus of the Fourier transform (FT) of the signal received by the antennas has the advantage of having a low computational cost. However, the local maxima do not necessarily correspond to the values of interest. To avoid this problem, we present an operation mode making it possible to address the estimations of the DOAs separately.
- Categories:
 23 Views
23 Views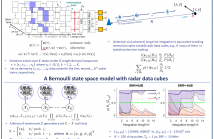
- Read more about Coherent long-time integration and Bayesian detection with Bernoulli track-before-detect
- Log in to post comments
We consider the problem of detecting small and manoeuvring objects with staring array radars. Coherent processing and long-time integration are key to addressing the undesirably low signal-to-noise/background conditions in this scenario and are complicated by the object manoeuvres. We propose a Bayesian solution that builds upon a Bernoulli state space model equipped with the likelihood of the radar data cubes through the radar ambiguity function. Likelihood evaluation in this model corresponds to coherent long-time integration.
- Categories:
 27 Views
27 Views