
- Read more about Compressed Quadratization of Higher Order Binary Optimization Problems
- Log in to post comments
Recent hardware advances in quantum and quantum-inspired annealers promise substantial speedup for solving NP-hard combinatorial optimization problems compared to general-purpose computers. These special-purpose hardware are built for solving hard instances of Quadratic Unconstrained Binary Optimization (QUBO) problems. In terms of number of variables and precision of these hardware are usually resource-constrained and they work either in Ising space $\ising$ or in Boolean space $\bool$. Many naturally occurring problem instances are higher-order in nature.
- Categories:
 56 Views
56 Views
- Read more about Multi-scale algorithms for optimal transport
- Log in to post comments
Optimal transport is a geometrically intuitive and robust way to quantify differences between probability measures.
It is becoming increasingly popular as numerical tool in image processing, computer vision and machine learning.
A key challenge is its efficient computation, in particular on large problems. Various algorithms exist, tailored to different special cases.
Multi-scale methods can be applied to classical discrete algorithms, as well as entropy regularization techniques. They provide a good compromise between efficiency and flexibility.
- Categories:
 23 Views
23 Views
- Read more about Convolutional group-sparse coding and source localization - Poster
- Log in to post comments
In this paper, we present a new interpretation of non-negatively constrained convolutional coding problems as blind deconvolution problems with spatially variant point spread function. In this light, we propose an optimization framework that generalizes our previous work on non-negative group sparsity for convolutional models. We then link these concepts to source localization problems that arise in scientific imaging, and provide a visual example on an image derived from data captured by the Hubble telescope.
- Categories:
 39 Views
39 Views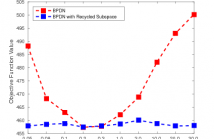
- Read more about ADMM Penalty Parameter Selection with Krylov Subspace Recycling Technique for Sparse Coding
- Log in to post comments
The alternating direction method of multipliers (ADMM) has been widely used for a very wide variety of imaging inverse problems. One of the disadvantages of this method, however, is the need to select an algorithm parameter, the penalty parameter, that has a significant effect on the rate of convergence of the algorithm. Although a number of heuristic methods have been proposed, as yet there is no general theory providing a good choice of this parameter for all problems.
- Categories:
 27 Views
27 ViewsEmbedding the l1 norm in gradient-based adaptive filtering is a popular solution for sparse plant estimation. Supported on the modal analysis of the adaptive algorithm near steady state, this work shows that the optimal sparsity tradeoff depends on filter length, plant sparsity and signal-to-noise ratio. In a practical implementation, these terms are obtained with an unsupervised mechanism tracking the filter weights. Simulation results prove the robustness and superiority of the novel adaptive-tradeoff sparsity-aware method.
- Categories:
 16 Views
16 Views