- Read more about Distinguished Lecture: IOT, Data and Healthcare: How do we get it right
- Log in to post comments
Abstract
DL_Wendy.pdf
- Categories:
 18 Views
18 Views- Read more about SoA-Fog: A Secure Service-Oriented Edge Computing Architecture for Smart Health Big Data Analytics
- Log in to post comments
- Categories:
 11 Views
11 Views- Read more about Smart Fog: Fog Computing Framework for Telehealth Big Data Analytics in Wearable Internet of Things
- Log in to post comments
- Categories:
 8 Views
8 ViewsLarge scale images allow pathologists to perform reviews, using
computer workstations instead of microscopes. This trend raises
a wide range of issues related to the management of these massive
datasets. In particular, efficient solutions for data storage and processing
have to be developed in order to deliver increasingly reliable
and faster analyses. In addition, the improvement of workflows also
requires the reinforcement of visualization capabilities. In this paper,
we present a new virtual microscopy (VM) approach for interactivetime
- Categories:
 15 Views
15 Views
- Read more about Summarization of Human Activity Videos Using a Salient Dictionary
- Log in to post comments
Video summarization has become more prominent during the last decade, due to the massive amount of available digital video content. A video summarization algorithm is typically fed an input video and expected to extract a set of important key-frames which represent the entire content, convey semantic meaning and are significantly more concise than the original input. The most wide-spread approach relies on video frame clustering and extraction of the frames closest to the cluster centroids as key-frames.
- Categories:
 15 Views
15 Views
- Read more about Multimodal Stereoscopic Movie Summarization Conforming to Narrative Characteristics
- Log in to post comments
Video summarization is a timely and rapidly developing research field with broad commercial interest, due to the increasing availability of massive video data. Relevant algorithms face the challenge of needing to achieve a careful balance between summary compactness, enjoyability and content coverage. The specific case of stereoscopic $3$D theatrical films has become more important over the past years, but not received corresponding research attention.
- Categories:
 11 Views
11 Views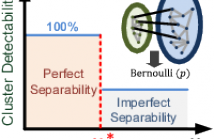
- Read more about AMOS: An Automated Model Order Selection Algorithm for Spectral Graph Clustering
- Log in to post comments
One of the longstanding problems in spectral graph clustering (SGC) is the so-called model order selection problem: automated selection of the correct number of clusters. This is equivalent to the problem of finding the number of connected components or communities in an undirected graph. In this paper, we propose AMOS, an automated model order selection algorithm for SGC.
- Categories:
 113 Views
113 Views
- Read more about Summarization of Human Activity Videos Via Low-Rank Approximation
- Log in to post comments
Summarization of videos depicting human activities is a timely problem with important applications, e.g., in the domains of surveillance or film/TV production, that steadily becomes more relevant. Research on video summarization has mainly relied on global clustering or local (frame-by-frame) saliency methods to provide automated algorithmic
- Categories:
 1 Views
1 Views
- Read more about Summarization of Human Activity Videos Via Low-Rank Approximation
- Log in to post comments
Summarization of videos depicting human activities is a timely problem with important applications, e.g., in the domains of surveillance or film/TV production, that steadily becomes more relevant. Research on video summarization has mainly relied on global clustering or local (frame-by-frame) saliency methods to provide automated algorithmic
- Categories:
 1 Views
1 Views
- Read more about Summarization of Human Activity Videos Via Low-Rank Approximation
- Log in to post comments
Summarization of videos depicting human activities is a timely problem with important applications, e.g., in the domains of surveillance or film/TV production, that steadily becomes more relevant. Research on video summarization has mainly relied on global clustering or local (frame-by-frame) saliency methods to provide automated algorithmic
- Categories:
 2 Views
2 Views