
- Read more about Dataset Culling: Towards Efficient Training of Distillation-based Domain Specific Models
- Log in to post comments
- Categories:
 37 Views
37 Views
- Read more about LEARNING GEOGRAPHICALLY DISTRIBUTED DATA FOR MULTIPLE TASKS USING GENERATIVE ADVERSARIAL NETWORKS
- Log in to post comments
We present a novel method that supports the learning of multiple classification tasks from geographically distributed data. By combining locally trained generative adversarial networks (GANs) with a small fraction of original data samples, our proposed scheme can train multiple discriminative models at a central location with low communication overhead. Experiments using common image datasets (MNIST, CIFAR-10, LSUN-20, Celeb-A) show that our proposed scheme can achieve comparable classification accuracy as the ideal classifier trained using all data from all sites.
poster-v1.pdf
- Categories:
 39 Views
39 Views
- Read more about A Stochastic LBFGS Algorithm for Radio Interferometric Calibration
- Log in to post comments
We present a stochastic, limited-memory Broyden Fletcher Goldfarb Shanno (LBFGS) algorithm that is suitable for handling very large amounts of data. A direct application of this algorithm is radio interferometric calibration of raw data at fine time and frequency resolution. Almost all existing radio interferometric calibration algorithms assume that it is possible to fit the dataset being calibrated into memory. Therefore, the raw data is averaged in time and frequency to reduce its size by many orders of magnitude before calibration is performed.
lofar78.pdf
- Categories:
 53 Views
53 Views
- Read more about A Characterization of Stochastic Mirror Descent Algorithms and Their Convergence Properties
- Log in to post comments
Stochastic mirror descent (SMD) algorithms have recently garnered a great deal of attention in optimization, signal processing, and machine learning. They are similar to stochastic gradient descent (SGD), in that they perform updates along the negative gradient of an instantaneous (or stochastically chosen) loss function. However, rather than update the parameter (or weight) vector directly, they update it in a "mirrored" domain whose transformation is given by the gradient of a strictly convex differentiable potential function.
- Categories:
 48 Views
48 Views
- Read more about MATRIX COMPLETION WITH VARIATIONAL GRAPH AUTOENCODERS: APPLICATION IN HYPERLOCAL AIR QUALITY INFERENCE
- Log in to post comments
Inferring air quality from a limited number of observations is an essential task for monitoring and controlling air pollution. Existing inference methods typically use low spatial resolution data collected by fixed monitoring stations and infer the concentration of air pollutants using additional types of data, e.g., meteorological and traffic information. In this work, we focus on street-level air quality inference by utilizing data collected by mobile stations.
- Categories:
 24 Views
24 Views
- Read more about Kernel Random Matrices of Large Concentrated Data: The Example of GAN-Generated Images
- Log in to post comments
Based on recent random matrix advances in the analysis of kernel methods for classification and clustering, this paper proposes the study of large kernel methods for a wide class of random inputs, i.e., concentrated data, which are more generic than Gaussian mixtures. The concentration assumption is motivated by the fact that one can use generative models to design complex data structures, through Lipschitz-ally transformed concentrated vectors (e.g., Gaussian) which remain concentrated vectors.
- Categories:
 24 Views
24 Views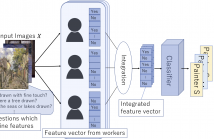
- Read more about CrowNN: Human-in-the-loop Network with Crowd-generated Inputs
- Log in to post comments
Input features are indispensable for almost all machine learning methods; however, their definitions themselves are sometimes too abstract to extract automatically. Human-in-the- loop machine learning is a promising solution to such cases where humans extract the feature values for machine learning models. We use crowdsourcing for feature value extraction and consider a problem to aggregate the feature values to improve machine learning classifiers.
- Categories:
 102 Views
102 Views
In this research, we aim to propose a data preprocessing framework particularly for financial sector to generate the rating data as input to the collaborative system. First, clustering technique is applied to cluster all users based on their demographic information which might be able to differentiate the customers’ background. Then, for each customer group, the importance of demographic characteristics which are highly associated with financial products purchasing are analyzed by the proposed fuzzy integral technique.
- Categories:
 14 Views
14 Views

- Read more about BEYOND WORD-LEVEL TO SENTENCE-LEVEL SENTIMENT ANALYSIS FOR FINANCIAL REPORTS
- Log in to post comments
- Categories:
 136 Views
136 Views