Sorry, you need to enable JavaScript to visit this website.

The goal of grammar compression is to construct a small sized context free grammar which uniquely generates the input text data. Among grammar compression methods, RePair is known for its good practical compression performance. MR-RePair was recently proposed as an improvement to RePair for constructing small-sized context free grammar for repetitive text data. However, a compact encoding scheme has not been discussed for MR-RePair. We propose a practical encoding method for MR-RePair and show its effectiveness through comparative experiments.

We introduce the problem of computing a parsing where each phrase is of length at most m and which minimizes the zeroth order entropy of parsing. Based on the recent theoretical results we devise a heuristic for this problem. The solution has straightforward application in succinct text representations and gives practical improvements. Moreover the proposed heuristic yields structure which size can be bounded both by |S|H_{m-1}(S) and by |S|/m(H_0(S) + ... + H_{m-1}(S)),where H_{k}(S) is the k-th order empirical entropy of S.

Single-pixel camera (SPC) captures encoded projections of the scene in a unique detector such that the number of compressive projections is lower than the size of the image. Traditionally, classification is not performed in the compressive domain because it is necessary to recover the underlying image before to classification. Based on the success of Deep Learning (DL) in classification approaches, this paper proposes to classify images using compressive measurements of SPC.

In modern video codecs, video frames are coded out-of-order following a hierarchical coding structure. The naive uniform video denoising, where denoising is applied indifferently to each frame, does not improve the compression performance. In our work, we only apply denoising to frames at layer 0 and 1. The denoising leads to a significant reduction of bit rates while maintaining temporal correlation. PSNR scores of the filtered frames decrease but PSNR scores of the unfiltered frames remain or even improve.

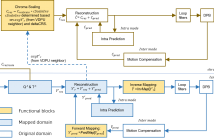
This paper describes a new video coding tool in the Versatile Video Coding standard (VVC) named as luma mapping with chroma scaling (LMCS). Experimental compression performance results for LMCS and non-normative examples for deriving LMCS parameter values are also provided. LMCS has two main components: 1) a process for mapping input luma code values to a new set of code values for use inside the coding loop; and 2) a luma-dependent process for scaling chroma residue values.

In order to achieve highly compact representation for videos, we propose an adaptive quantization based perceptual video coding (PVC) scheme in this paper. Because human only perceive the limited discrete-scale quality levels, the perceptual quantization is transformed into the problem of how to determine the maximum quantization parameter (Qp) under the same perceptual quality level. So, the relationship between perceptual quality level and quantization parameter is analyzed with the statistical way in this paper.

This paper introduces the de Bruijn graph edge minimization problem, which is related to the compression of de Bruijn graphs: find the order-k de Bruijn graph with minimum edge count among all orders. We describe an efficient algorithm that solves this problem. Since the edge minimization problem is connected to the BWT compression technique called "tunneling", the paper also describes a way to minimize the length of a tunneled BWT in such a way that useful properties for sequence analysis are preserved.

Huffman coding is known to be optimal in case the alphabet is known in advance, the set of codewords is fixed and each codeword consists of an integral number of bits. If one of these conditions is violated, optimality is not guaranteed.
In the {\it dynamic\/} variant of Huffman coding the encoder and decoder maintain identical copies of the model; at each position, the model consists of the frequencies of the elements processed so far.