
- Read more about Assessing cross-dependencies using bivariate multifractal analysis
- Log in to post comments
Multifractal analysis, notably with its recent wavelet-leader based formulation, has nowadays become a reference tool to characterize scale-free temporal dynamics in time series. It proved successful in numerous applications very diverse in nature. However, such successes remained restricted to univariate analysis while many recent applications call for the joint analysis of several components. Surprisingly, multivariate multifractal analysis remained mostly overlooked.
- Categories:
 9 Views
9 Views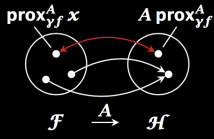
- Read more about A Theory of Generalized Proximity for ADMM
- Log in to post comments
The alternating direction method of multipliers has become in recent years the most widely used proximal method for signal processing. In this paper, we lay the groundwork for a new notion of proximity and use it to illustrate that the method (ADMM) is actually somewhat of a maladroit rearrangement of a new, more practical procedure that generalizes the Douglas-Rachford algorithm. Compared to ADMM, the algorithm that we propose enjoys not only a more sensible form, but also a more general convergence result.
Poster.pdf
- Categories:
 19 Views
19 Views- Read more about ON THE CONVERGENCE OF CONSTRAINED PARTICLE FILTERS
- Log in to post comments
The power of particle filters in tracking the state of non-linear and non-Gaussian systems stems not only from their simple numerical implementation but also from their optimality and convergence properties. In particle filtering, the posterior distribution of the state is approximated by a discrete mass of samples, called particles, that stochastically evolve in time according to the dynamics of the model and the observations. Particle filters have been shown to converge almost surely toward the optimal filter as the number of particles increases.
- Categories:
 28 Views
28 Views- Read more about APPROXIMATE SIMULATION OF LINEAR CONTINUOUS TIME MODELS DRIVEN BY ASYMMETRIC STABLE LÉVY PROCESSES
- Log in to post comments
In this paper we extend to the multidimensional case the modified Poisson series representation of linear stochastic processes driven by $\alpha$-stable innovations. The latter has been recently introduced in the literature and it involves a Gaussian approximation of the residuals of the series, via the exact characterization of their moments. This allows for Bayesian techniques for parameter or state inference that would not be available otherwise, due to the lack of a closed-form likelihood function for the $\alpha$-stable distribution.
ICASSP.pdf
- Categories:
 16 Views
16 ViewsThe paper introduces a novel class of complex nonlinear filters, the complex functional link polynomial (CFLiP) filters.
These filters present many interesting properties. They are a sub-class of linear-in-the-parameter nonlinear filters.
They satisfy all the conditions of Stone-Weirstrass theorem and thus are universal approximators for causal, time-invariant, discrete-time, finite-memory, complex, continuous systems defined on a compact domain.
- Categories:
 7 Views
7 Views
- Read more about A Fast Iterative Algorithm for Demixing Sparse Signals from Nonlinear Observations
- Log in to post comments
In this paper, we propose an iterative algorithm based on hard thresholding
for demixing a pair of signals from nonlinear observations of
their superposition. We focus on the under-determined case where
the number of available observations is far less than the ambient dimension
of the signals. We derive nearly-tight upper bounds on the
sample complexity of the algorithm to achieve stable recovery of the
component signals. Moreover, we show that the algorithm enjoys
a linear convergence rate. We provide a range of simulations to illustrate
- Categories:
 8 Views
8 Views
- Read more about Robust Estimation of Self-Exciting Point Process Models with Application to Neuronal Modeling
- Log in to post comments
We consider the problem of estimating discrete self- exciting point process models from limited binary observations, where the history of the process serves as the covariate. We analyze the performance of two classes of estimators: l1-regularized maximum likelihood and greedy estimation for a discrete version of the Hawkes process and characterize the sampling tradeoffs required for stable recovery in the non-asymptotic regime. Our results extend those of compressed sensing for linear and generalized linear models with i.i.d.
- Categories:
 19 Views
19 Views- Read more about A Bayesian framework for the multifractal analysis of images using data augmentation and a Whittle approximation
- Log in to post comments
Texture analysis is an image processing task that can be conducted using the mathematical framework of multifractal analysis to study the regularity fluctuations of image intensity and the practical tools for their assessment, such as (wavelet) leaders. A recently introduced statistical model for leaders enables the Bayesian estimation of multifractal parameters. It significantly improves performance over standard (linear regression based) estimation. However, the computational cost induced by the associated nonstandard posterior distributions limits its application.
- Categories:
 12 Views
12 Views- Read more about PARAMETER ESTIMATION OF POLYNOMIAL PHASE SIGNAL BASED ON LOW-COMPLEXITY LSU-EKF ALGORITHM IN ENTIRE IDENTIFIABLE REGION
- Log in to post comments
Fast implementation of parameter estimation for polynomial phase signal (PPS) is considered in this paper. A method which combines the least squares unwrapping (LSU) estimator and the extended Kalman filter (EKF) is proposed. A small number of initial samples are used to estimate the PPS’s parameters and then these coarse estimates are used to initial the EKF. The proposed LSU-EKF estimator greatly reduces the computation complexity of the LSU estimator and can work in entire identifiable region which inherits from the LSU estimator.
- Categories:
 8 Views
8 Views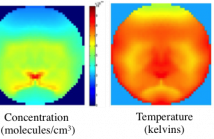
- Read more about Gaussian Mixture Prior Models for Imaging of Flow Cross Sections from Sparse Hyperspectral Measurements
- Log in to post comments
This is an overview presentation about developing accurate prior models that can capture non-Gaussian characteristics of images. The slides use tunable diode laser absorption tomography (TDLAT) as an application to show the results.
For more information, please check out the publication at IEEE Xplore:
Zeeshan Nadir, Michael S. Brown, Mary L. Comer, Charles A. Bouman, “Gaussian Mixture Prior Models for Imaging of Flow Cross Sections from Sparse Hyperspectral Measurements” , 2015 IEEE GlobalSIP Conference, Dec 14-16
- Categories:
 12 Views
12 Views