
- Read more about MAP-informed Unrolled Algorithms for Hyper-parameter Estimation
- Log in to post comments
Hyper-parameter tuning, and especially regularisation parameter estimation, is a challenging but essential task when solving inverse problems. The solution is obtained here through the minimization of a functional composed of a data fidelity term and a regularization term. Those terms are balanced through a (or several) regularisation parameter(s) whose estimation is made under an unrolled strategy together with the inverse problem solving. The resulting network is
ICIP_oral.pdf
- Categories:
 43 Views
43 Views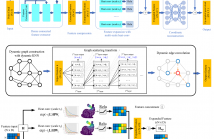
- Read more about Point Cloud Upsampling via Dynamic Graph Scattering Transform
- Log in to post comments
Point cloud upsampling is a challenging task to generate dense and uniform point clouds from sparse and irregular inputs. Existing deep learning based methods usually leverage graph convolution networks (GCNs) to learn features for expansion and reconstruction but suffer from the over-smoothing issue by discarding the high-frequency components. In this paper, we design a novel dynamic graph scattering transform (GST) to achieve multi-scale feature extraction for point cloud upsampling.
poster.pptx
- Categories:
 34 Views
34 Views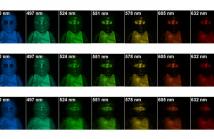
- Read more about Optimized Coded Aperture Design in Compressive Spectral Imaging via Coherence Minimization
- Log in to post comments
The coded aperture snapshot spectral imager (CASSI) system senses spatial and spectral information using a binary coded aperture and a dispersive element, thus the quality of reconstructed hyperspectral images is mainly determined by the structure of coded apertures. Traditional coded apertures (Random, Bernoulli, etc.), encoding hyperspectral images in focal array plane, suffer from suboptimal reconstruction accuracy. Therefore, optimizing coded aperture design improves the reconstruction quality for the scene.
- Categories:
 108 Views
108 Views
- Read more about Fast Robust Principle Component Analysis using Gauss-Newton Iterations
- Log in to post comments
Robust Principal Component Analysis (RPCA) is an optimization problem that decomposes a data matrix into a low-rank and a sparse matrix. However, solving this problem using alternating procedures requires sequentially computing singular value decompositions (SVDs) of large matrices, which is computationally expensive. In this work, we propose a computation protocol that leverages Gauss-Newton iterations to speed up the sequential computation of SVDs and accelerate the entire RPCA process.
- Categories:
 20 Views
20 Views
- Read more about LiQuiD-MIMO Radar: Distributed MIMO Radar with Low-Bit Quantization
- Log in to post comments
Distributed MIMO radar is known to achieve superior sensing performance by employing widely separated antennas. However, it is challenging to implement a low-complexity distributed MIMO radar due to the complex operations at both the receivers and the fusion center. This work proposes a low-bit quantized distributed MIMO (LiQuiDMIMO) radar to significantly reduce the burden of signal acquisition and data transmission. In the LiQuiD-MIMO radar, the widely-separated receivers are restricted to operating with low-resolution ADCs and deliver the low-bit quantized data to the fusion center.
- Categories:
 51 Views
51 Views
- Read more about REGRESSION TO CLASSIFICATION: WAVEFORM ENCODING FOR NEURAL FIELD-BASED AUDIO SIGNAL REPRESENTATION
- Log in to post comments
Neural fields, also known as coordinate-based representations, are an emerging signal representation framework. This approach has also been used to represent audio signals, but the generated audio often contains noise. To reduce noise and improve representation quality, we propose using waveform encoding in the neural field. Instead of yielding real numbers for each temporal coordinate, this involves using discrete integers as outputs, with waveform-encoded integers as target classes, and treating the representation problem as a classification task rather than a regression problem.
- Categories:
 16 Views
16 Views
- Read more about Data-Driven Algorithms for Gaussian Measurement Matrix Design in Compressive Sensing
- Log in to post comments
In this paper, we provide two data-driven algorithms for learning compressive sensing measurement matrices with Gaussian entries. In contrast to the ubiquitous i.i.d.~Gaussian design, we associate different variances with different signal entries, so that we may utilize training data to focus more energy on the ``most important'' parts of the signal.
- Categories:
 16 Views
16 Views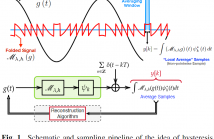
- Read more about Unlimited Sampling with Local Averages
- Log in to post comments
Analog-to-digital converters (ADCs) are known to suffer from saturation and clipping for inputs exceeding their dynamic range (DR). Recently, the Unlimited Sampling approach addressed this problem by inserting a modulo non-linearity between the input and the ADC. Moreover, a new model called modulo-hysteresis was introduced to enable the recovery of different classes of inputs from noisy observations. ADCs are typically assumed to acquire the instantaneous input amplitude via an inner product with a Dirac delta function.
- Categories:
 44 Views
44 Views
The projection of sample measurements onto a reconstruction space represented by a basis on a regular grid is a powerful and simple approach to estimate a probability density function. In this paper, we focus on Riesz bases and propose a projection operator that, in contrast to previous works, guarantees the bona fide properties for the estimate, namely, non-negativity and total probability mass 1. Our bona fide projection is defined as a convex problem. We propose solution techniques and evaluate them.
- Categories:
 20 Views
20 Views
- Read more about Bona fide Riesz projections for density estimation - Presentation
- Log in to post comments
The projection of sample measurements onto a reconstruction space represented by a basis on a regular grid is a powerful and simple approach to estimate a probability density function. In this paper, we focus on Riesz bases and propose a projection operator that, in contrast to previous works, guarantees the bona fide properties for the estimate, namely, non-negativity and total probability mass 1. Our bona fide projection is defined as a convex problem. We propose solution techniques and evaluate them.
- Categories:
 17 Views
17 Views