- Communication and Sensing aspects of Sensor Networks, Wireless and Ad-Hoc Networks
- Communication Systems and Applications
- MIMO Communications and Signal Processing
- Signal Transmission and Reception
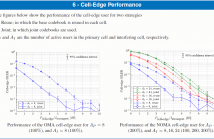
- Read more about Joint Codebook Design for Multi-Cell NOMA
- Log in to post comments
For spreading-based multiple access, whether orthogonal (OMA) or non-orthogonal (NOMA), the spreading sequences (signatures) are selected from a predefined codebook. When operating in a cellular system, intercell interference will be inherently present between close base stations that share the same resources. If the codebook is reused across the different cells, then intercell interference can cause a full collision of the interfering users in the code-domain, thus deteriorating their performance, especially those at the cell-edge.
- Categories:
 49 Views
49 Views
- Read more about Polar Feature Based Deep Architectures for Automatic Modulation Classification Considering Channel Fading
- Log in to post comments
To develop intelligent receivers, automatic modulation classification (AMC) plays an important role for better spectrum utilization. The emerging deep learning (DL) technique has received much attention in AMC due to its superior performance in classifying data with deep structure. In this work, a novel polar-based deep learning architecture with channel compensation network (CCN) is proposed. Our test results show that learning features from polar domain (r-θ) can improve recognition accuracy by 5% and reduce training overhead by 48%.
- Categories:
 12 Views
12 Views
- Read more about Generalized Graph Signal Processing
- Log in to post comments
Globalsip.pdf
- Categories:
 20 Views
20 Views
- Read more about Flexible Infrastructure for the Development and Integration of Access / Fronthauling Solutions in Future Wireless Systems
- Log in to post comments
The deployment of the 5G technology(ies) is planned to start by 2020, and these future systems will comprise multiple heterogeneous technologies and services ranging from the personal cellular, wireless local area networks (WLAN) up to the Internet of Things (IoT). The inherent complexity and heterogeneity in technology conjugated with the random nature of both the wireless channel, access and services will make the system evaluation of 5G a very difficult task calling for flexible testbeds where the randomness of the radio environment and mobility can be realistically emulated.
- Categories:
 13 Views
13 Views

- Read more about Software Defined Resource Allocation for Service-Oriented Networks
- Log in to post comments
- Categories:
 5 Views
5 Views
- Read more about Sparsity and Rank Exploitation for Time-Varying Narrowband Leaked OFDM Channel Estimation
- Log in to post comments
In this paper, the problem of time-varying narrowband leaked Orthogonal Frequency Division multiplexing (OFDM) channel estimation is considered. The leakage effect results from practical constraints on communication systems: finite bandwidth and block length. These practical constraints effectively render a sparse channel into a non-sparse one. The inherent low-rank structure of the received signal, determined by the number of dominant paths of the channel, is exploited.
- Categories:
 24 Views
24 Views
- Read more about Small Perturbation Analysis of Network Topologies
- Log in to post comments
ICASSP2018.pdf
- Categories:
 31 Views
31 Views
- Read more about Optimal Tone Reservation for Peak to Average Power Control of CDMA Systems
- Log in to post comments
In this paper we study the tone reservation technique for the reduction of the peak to average power ratio (PAPR) in code division multiple access (CDMA) systems that employ the Walsh functions. In the tone reservation method, the available carriers are partitioned into two sets, the information set, which carries the information, and the compensation set, which is used to reduce the PAPR. Central questions are: What is the best possible reduction of the PAPR? What is the optimal information set that achieves this reduction, and how can it be found?
- Categories:
 67 Views
67 Views