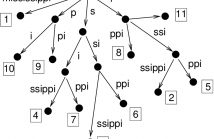
- Read more about Computing Matching Statistics on Wheeler DFAs
- Log in to post comments
Matching statistics were introduced to solve the approximate string matching problem, which is a recurrent subroutine in bioinformatics applications. In 2010, Ohlebusch et al. [SPIRE 2010] proposed a time and space efficient algorithm for computing matching statistics which relies on some components of a compressed suffix tree - notably, the longest common prefix (LCP) array.
- Categories:
 84 Views
84 Views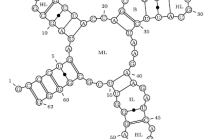
- Read more about RNA secondary structures: from ab initio prediction to better compression, and back
- Log in to post comments
In this paper, we use the biological domain knowledge incorporated into stochastic models
for ab initio RNA secondary-structure prediction to improve the state of the art in joint
compression of RNA sequence and structure data (Liu et al., BMC Bioinformatics, 2008).
Moreover, we show that, conversely, compression ratio can serve as a cheap and robust
proxy for comparing the prediction quality of different stochastic models, which may help
guide the search for better RNA structure prediction models.
- Categories:
 37 Views
37 Views
Lossless data compression algorithms were developed to shrink files. But these algorithms can also be used to measure file similarity. In this article, the meta-algorithms Concat Compress and Cross Compress are subjected to an extensive practical test together with the compression algorithms Re-Pair, gzip and bz2: Five labeled datasets are subjected to a classification procedure using these algorithms. Theoretical considerations about the two meta-algorithms were already made about 10 years ago, but little has happened since then.
- Categories:
 88 Views
88 Views
- Read more about Constructing the CDAWG CFG using LCP-Intervals
- Log in to post comments
It is known that a context-free grammar (CFG) that produces a single string can be derived from the compact directed acyclic word graph (CDAWG) for the same string. In this work, we show that the CFG derived from a CDAWG is deeply connected to the maximal repeat content of the string it produces and thus has O(m) rules, where m is the number of maximal repeats in the string. We then provide a generic algorithm based on this insight for constructing the CFG from the LCP-intervals of a string in O(n) time, where n is the length of the string.
- Categories:
 96 Views
96 Views- Read more about Graphs can be succinctly indexed for pattern matching in O(E^2 + V^{2.5}) time
- Log in to post comments
For the first time we provide a \emph{succinct} pattern matching index for \emph{arbitrary} graphs that can be built \emph{in polynomial time}, while improving both space and query time bounds from [SODA 2021].
- Categories:
 61 Views
61 Views- Read more about Linear-time minimization of Wheeler DFAs
- 2 comments
- Log in to post comments
Wheeler DFAs (WDFAs) are a sub-class of finite-state automata which is playing an important role in the emerging field of \emph{compressed data structures}: as opposed to general automata, WDFAs can be stored in just $\log\sigma + O(1)$ bits per edge, $\sigma$ being the alphabet's size, and support optimal-time pattern matching queries on the substring closure of the language they recognize. An important step to achieve further compression is minimization.
- Categories:
 139 Views
139 Views
- Read more about SortComp (Sort-and-Compress) - Towards a Universal Lossless Compression Scheme for Matrix and Tabular Data
- 1 comment
- Log in to post comments
A universal scheme is proposed for the lossless compression of two-dimensional tables and matrices. Instead of standard row- or column-based compression, we propose to sort each column first and record both the sorted table and the corresponding permutation table of the sorting permutations. These two tables are then separately compressed. In this new scheme, both intra- and inter-column correlations can be efficiently captured, giving rise to improved compression ratio in particular when both column-wise and row-wise dependencies cooccur.
- Categories:
 168 Views
168 Views
- Read more about Converting RLBWT to LZ77 in smaller space
- 1 comment
- Log in to post comments
RLBWT2LZ77.pdf
- Categories:
 56 Views
56 Views
- Read more about Compact Representation of Spatial Hierarchies and Topological Relationships
- Log in to post comments
The topological model for spatial objects identifies common boundaries between regions, explicitly storing adjacency relations, which not only improves the efficiency of topology-related queries, but also provides advantages such as avoiding data duplication and facilitating data consistency. Recently, a compact representation of the topological model based on planar graph embeddings was proposed.
- Categories:
 41 Views
41 Views