
While globally optimal solutions to many convex programs can be computed efficiently in polynomial time, this is, in general, not possible for nonconvex optimization problems. Therefore, locally optimal approaches or other efficient suboptimal heuristics are usually applied for practical implementations. However, there is also a strong interest in computing globally optimal solutions of nonconvex problems in offline simulations in order to benchmark faster suboptimal algorithms. Global solutions often rely on monotonicity properties.
- Categories:
 26 Views
26 Views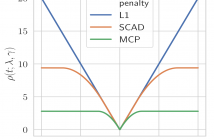
In this paper, we study the denoising of piecewise smooth graph sig-nals that exhibit inhomogeneous levels of smoothness over a graph. We extend the graph trend filtering framework to a family of non-convex regularizers that exhibit superior recovery performance overexisting convex ones. We present theoretical results in the form ofasymptotic error rates for both generic and specialized graph models. We further present an ADMM-based algorithm to solve the proposedoptimization problem and analyze its convergence.
- Categories:
 143 Views
143 Views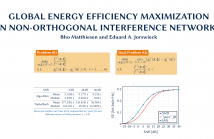
- Read more about Global Energy Efficiency Maximization in Non-Orthogonal Interference Networks
- Log in to post comments
Energy efficient resource allocation in interference networks is a challenging global optimization problem. The main issue is that the computational complexity grows exponentially in the number of variables. In general, resource allocation in interference networks requires optimizing jointly over achievable rates and transmit powers. However, close scrutiny reveals that the non-convexity stems mostly from the powers while the problem is linear in the rates.
- Categories:
 24 Views
24 Views
- Read more about Optimal Resource Allocation for Non-Regenerative Multiway Relaying with Rate Splitting
- Log in to post comments
Optimal resource allocation in interference networks requires the solution of non-convex optimization problems. Except from treating interference as noise (IAN) one usually has to optimize jointly over the achievable rates and transmit powers. This non-convexity is normally only due to the transmit powers while the rates are linear. Conventional approaches like the Polyblock Algorithm treat all variables equally and, thus, require a two layer solver to exploit the linearity in the rates and keep the computational complexity at a reasonable level.
poster.pdf
- Categories:
 21 Views
21 Views
- Read more about The Landscape of Non-convex Quadratic Feasibility
- Log in to post comments
Motivated by applications such as ordinal embedding and collaborative ranking, we formulate homogeneous quadratic feasibility as an unconstrained, non-convex minimization problem. Our work aims to understand the landscape (local minimizers and global minimizers) of the non-convex objective, which corresponds to hinge losses arising from quadratic constraints. Under certain assumptions, we give necessary conditions for non-global, local minimizers of our objective and additionally show that in two dimensions, every local minimizer is a global minimizer.
ICASSP_v4.pdf
- Categories:
 130 Views
130 Views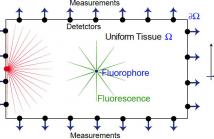
- Read more about Sparse Reconstruction for Fluorescence Lifetime Imaging Microscopy with Poisson Noise
- Log in to post comments
We present a novel, three-stage method to solve the fluorescence lifetime imaging problem under low-photon conditions. In particular, we reconstruct the fluorophore concentration along with its support and fluorescence lifetime from the time-dependent measurements of scattered light exiting the domain. Because detectors used for these problems are photon counting devices, measurements are corrupted by Poisson noise. Consequently, we explicitly consider Poisson noise in conjunction with SPIRAL-$\ell_p$ -- a sparsity-promoting nonconvex optimization method -- to solve this problem.
GlobalSIP.pdf
- Categories:
 16 Views
16 Views- Read more about Non-monotone Quadratic Potential Games with single Quadratic constraints
- Log in to post comments
We consider the problem of solving a quadratic potential game with single quadratic constraints, under no monotonicity condition of the game, nor convexity in any of the player's problem. We show existence of Nash equilibria (NE) in the game, and propose a framework to calculate Pareto efficient solutions. Regarding the corresponding non-convex potential function, we show that strong duality holds with its corresponding dual problem, give existence results of solutions and present conditions for global optimality. Finally, we propose a centralized method to solve the potential problem, and a distributed version for compact constraints. We also present simulations showing convergence behavior of the proposed distributed algorithm.
- Categories:
 7 Views
7 Views