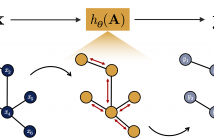
- Read more about Bayesian topology inference on partially known networks from input-output pairs
- Log in to post comments
We propose a sampling algorithm to perform system identification from a set of input-output graph signal pairs. The dynamics of the systems we study are given by a partially known adjacency matrix and a generic parametric graph filter of unknown parameters. The methodology we employ is built upon the principles of annealed Langevin diffusion. This enables us to draw samples from the posterior distribution instead of following the classical approach of point estimation using maximum likelihood.
- Categories:
 28 Views
28 Views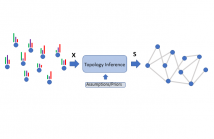
- Read more about Network Topology Inference from Gaussian and Stationary Graph Signals
- Log in to post comments
Graphs have become pervasive tools to represent information and datasets with irregular support. However, in many cases, the underlying graph is either unavailable or naively obtained, calling for more advanced methods for its estimation. Indeed, graph topology inference methods that estimate the network structure from a set of signal observations have a long and well-established history. By assuming that the observations are both Gaussian and stationary in the sought graph, this paper proposes a new scheme to learn the network from nodal observations.
- Categories:
 54 Views
54 Views
- Read more about Untrained graph neural networks for denoising
- Log in to post comments
A fundamental problem in signal processing is to denoise a signal. While there are many well-performing methods for denoising signals defined on regular domains, including images defined on a two-dimensional pixel grid, many important classes of signals are defined over irregular domains that can be conveniently represented by a graph. This paper introduces two untrained graph neural network architectures for graph signal denoising, develops theoretical guarantees for their denoising capabilities in a simple setup, and provides empirical evidence in more general scenarios.
- Categories:
 74 Views
74 Views
- Read more about Permutation Entropy for Graph Signals
- Log in to post comments
Entropy metrics (for example, permutation entropy) are nonlinear measures of irregularity in time series (one-dimensional data). Some of these entropy metrics can be generalised to data on periodic structures such as a grid or lattice pattern (two-dimensional data) using its symmetry, thus enabling their application to images. However, these metrics have not been developed for signals sampled on irregular domains, defined by a graph.
- Categories:
 35 Views
35 Views- Read more about An M-Channel Critically Sampled Graph Filter Bank
- Log in to post comments
We investigate an M-channel critically sampled filter bank for graph signals where each of the M filters is supported on a different subband of the graph Laplacian spectrum. We partition the graph vertices such that the mth set comprises a uniqueness set for signals supported on the mth subband. For analysis, the graph signal is filtered on each subband and downsampled on the corresponding set of vertices.
- Categories:
 30 Views
30 Views- Read more about A SHORT-GRAPH FOURIER TRANSFORM VIA PERSONALIZED PAGERANK VECTORS
- Log in to post comments
The short-time Fourier transform (STFT) is widely used to analyze the spectra of temporal signals that vary through time. Signals defined over graphs, due to their intrinsic complexity, exhibit large variations in their patterns. In this work we propose a new formulation for an STFT for signals defined over graphs. This formulation draws on recent ideas from spectral graph theory, using personalized PageRank vectors as its fundamental building block.
poster.pdf
- Categories:
 19 Views
19 Views