
- Read more about DEMUCS for data-driven RF signal denoising
- Log in to post comments
In this paper, we present our radio frequency signal denoising approach, RFDEMUCS, for the 2024 IEEE ICASSP RF Signal Separation Challenge. Our approach is based on the DEMUCS architecture [1], and has a U-Net structure with a bidirectional LSTM bottleneck. For the task of estimating the underlying bit-sequence message, we also propose an extension of the DEMUCS that directly estimates the bits. Evaluations of the presented methods on the challenge test dataset yield MSE and BER scores of −118.71 and −81, respectively, according to the evaluation metrics defined in the challenge.
- Categories:
 79 Views
79 Views
- Read more about PENDANTSS: PEnalized Norm-Ratios Disentangling Additive Noise, Trend and Sparse Spikes
- Log in to post comments
Denoising, detrending, deconvolution: usual restoration tasks, traditionally decoupled. Coupled formulations entail complex ill-posed inverse problems. We propose PENDANTSS for joint trend removal and blind deconvolution of sparse peak-like signals. It blends a parsimonious prior with the hypothesis that smooth trend and noise can somewhat be separated by low-pass filtering.
- Categories:
 83 Views
83 Views- Read more about Joint Unmixing And Demosaicing Methods For Snapshot Spectral Images
- Log in to post comments
Recent technological advances in design and processing speed have successfully demonstrated a new snapshot mosaic imaging sensor architecture (SSI), allowing miniaturized platforms to efficiently acquire the spatio-spectral content of the dynamic scenes from a single exposure. However, SSI systems have a fundamental trade-off between spatial and spectral resolution because they associate each pixel with a specific spectral band.
- Categories:
 58 Views
58 Views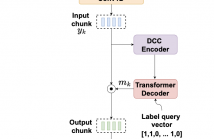
- Read more about Real-Time Target Sound Extraction
- Log in to post comments
We present the first neural network model to achieve real-time and streaming target sound extraction. To accomplish this, we propose Waveformer, an encoder-decoder architecture with a stack of dilated causal convolution layers as the encoder, and a transformer decoder layer as the decoder. This hybrid architecture uses dilated causal convolutions for processing large receptive fields in a computationally efficient manner, while also leveraging the generalization performance of transformer-based architectures.
- Categories:
 46 Views
46 Views
- Read more about HARMONICITY PLAYS A CRITICAL ROLE IN DNN BASED VERSUS IN BIOLOGICALLY-INSPIRED MONAURAL SPEECH SEGREGATION SYSTEMS
- Log in to post comments
Recent advancements in deep learning have led to drastic improvements in speech segregation models. Despite their success and growing applicability, few efforts have been made to analyze the underlying principles that these networks learn to perform segregation. Here we analyze the role of harmonicity on two state-of-the-art Deep Neural Networks (DNN)-based models- Conv-TasNet and DPT-Net. We evaluate their performance with mixtures of natural speech versus slightly manipulated inharmonic speech, where harmonics are slightly frequency jittered.
Parikh_poster.pdf
Parikh_CR.pdf
- Categories:
 16 Views
16 Views
- Read more about BLIND UNMIXING USING A DOUBLE DEEP IMAGE PRIOR
- Log in to post comments
ICASSP2022.pdf
- Categories:
 12 Views
12 Views
- Read more about BLIND UNMIXING USING A DOUBLE DEEP IMAGE PRIOR
- Log in to post comments
Poster.pdf
- Categories:
 8 Views
8 Views
- Read more about ICASSP21 Poster of `Nonnegative Unimodal Matrix Factorization'
- Log in to post comments
We introduce a new Nonnegative Matrix Factorization (NMF) model called Nonnegative Unimodal Matrix Factorization (NuMF), which adds on top of NMF the unimodal condition on the columns of the basis matrix. NuMF finds applications for example in analytical chemistry. We propose a simple but naive brute-force heuristics strategy based on accelerated projected gradient. It is then improved by using multi-grid for which we prove that the restriction operator preserves the unimodality.
- Categories:
 14 Views
14 Views
- Read more about SANDGLASSET: A LIGHT MULTI-GRANULARITY SELF-ATTENTIVE NETWORK FOR TIME-DOMAIN SPEECH SEPARATION
- Log in to post comments
One of the leading single-channel speech separation (SS) models is based on a TasNet with a dual-path segmentation technique, where the size of each segment remains unchanged throughout all layers. In contrast, our key finding is that multi-granularity features are essential for enhancing contextual modeling and computational efficiency. We introduce a self-attentive network with a novel sandglass-shape, namely Sandglasset, which advances the state-of-the-art (SOTA) SS performance at significantly smaller model size and computational cost.
- Categories:
 31 Views
31 Views
- Read more about ENHANCING END-TO-END MULTI-CHANNEL SPEECH SEPARATION VIA SPATIAL FEATURE LEARNING
- Log in to post comments
Hand-crafted spatial features (e.g., inter-channel phase difference, IPD) play a fundamental role in recent deep learning based multi-channel speech separation (MCSS) methods. However, these manually designed spatial features are hard to incorporate into the end-to-end optimized MCSS framework. In this work, we propose an integrated architecture for learning spatial features directly from the multi-channel speech waveforms within an end-to-end speech separation framework. In this architecture, time-domain filters spanning signal channels are trained to perform adaptive spatial filtering.
- Categories:
 115 Views
115 Views