
- Read more about CORRENTROPY-BASED ADAPTIVE FILTERING OF NONCIRCULAR COMPLEX DATA
- Log in to post comments
- Categories:
 14 Views
14 Views
- Read more about DATA CENSORING WITH SET-MEMBERSHIP ALGORITHMS
- Log in to post comments
In this paper, we use the set-membership normalized least-mean-square (SM-NLMS) algorithm to censor the data set in big data applications. First, we use the distribution of the noise signal and the excess of the steady-state mean-square error (EMSE) to estimate the threshold for the desired update rate in the single threshold SM-NLMS (ST-SM-NLMS) algorithm. Then, we introduce the double threshold SM-NLMS (DT-SM-NLMS) algorithm which defines an acceptable
range of the error signal. This algorithm censors the data with very low and very high output estimation error.
- Categories:
 25 Views
25 Views- Read more about The Adaptive Complex Shock Diffusion for Seismic Random Noise Attenuation
- Log in to post comments
- Categories:
 12 Views
12 Views- Read more about D2L: DECENTRALIZED DICTIONARY LEARNING OVER DYNAMIC NETWORKS
- Log in to post comments
D4L_slides.pdf
- Categories:
 8 Views
8 Views- Read more about RECURSIVE LEAST-SQUARES ALGORITHMS FOR SPARSE SYSTEM MODELING
- Log in to post comments
In this paper, we propose some sparsity aware algorithms, namely the Recursive least-Squares for sparse systems (S-RLS) and l0-norm Recursive least-Squares (l0-RLS), in order to exploit the sparsity of an unknown system. The first algorithm, applies a discard function on the weight vector to disregard the coefficients close to zero during the update process. The second algorithm, employs the sparsity-promoting scheme via some non-convex approximations to the l0-norm.
- Categories:
 13 Views
13 Views
Spike and Slab priors have been of much recent interest in signal processing as a means of inducing sparsity in Bayesian inference. Applications domains that benefit from the use of these priors include sparse recovery, regression and classification. It is well-known that solving for the sparse coefficient vector to maximize these priors results in a hard non-convex and mixed integer programming problem. Most existing solutions to this optimization problem either involve simplifying assumptions/relaxations or are computationally expensive.
- Categories:
 18 Views
18 Views
- Read more about Robust Estimation of Self-Exciting Point Process Models with Application to Neuronal Modeling
- Log in to post comments
We consider the problem of estimating discrete self- exciting point process models from limited binary observations, where the history of the process serves as the covariate. We analyze the performance of two classes of estimators: l1-regularized maximum likelihood and greedy estimation for a discrete version of the Hawkes process and characterize the sampling tradeoffs required for stable recovery in the non-asymptotic regime. Our results extend those of compressed sensing for linear and generalized linear models with i.i.d.
- Categories:
 19 Views
19 Views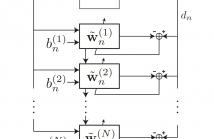
We introduce in this paper the recursive Hessian sketch, a new adaptive filtering algorithm based on sketching the same exponentially weighted least squares problem solved by the recursive least squares algorithm. The algorithm maintains a number of sketches of the inverse autocorrelation matrix and recursively updates them at random intervals. These are in turn used to update the unknown filter estimate. The complexity of the proposed algorithm compares favorably to that of recursive least squares.
- Categories:
 19 Views
19 Views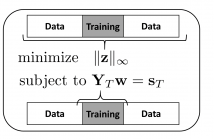
- Read more about Compressed Training Adaptive Equalization
- Log in to post comments
We introduce it compressed training adaptive equalization as a novel approach for reducing number of training symbols in a communication packet. The proposed semi-blind approach is based on the exploitation of the special magnitude boundedness of communication symbols. The algorithms are derived from a special convex optimization setting based on l_\infty norm. The corresponding framework has a direct link with the compressive sensing literature established by invoking the duality between l_1 and l_\infty norms.
- Categories:
 23 Views
23 ViewsEmbedding the l1 norm in gradient-based adaptive filtering is a popular solution for sparse plant estimation. Supported on the modal analysis of the adaptive algorithm near steady state, this work shows that the optimal sparsity tradeoff depends on filter length, plant sparsity and signal-to-noise ratio. In a practical implementation, these terms are obtained with an unsupervised mechanism tracking the filter weights. Simulation results prove the robustness and superiority of the novel adaptive-tradeoff sparsity-aware method.
- Categories:
 16 Views
16 Views