
- Read more about DISTRIBUTED STOCHASTIC CONTEXTUAL BANDITS FOR PROTEIN DRUG INTERACTION
- Log in to post comments
In recent work [1], we developed a distributed stochastic multi-arm contextual bandit algorithm to learn optimal actions when the contexts are unknown, and M agents work collaboratively under the coordination of a central server to minimize the total regret. In our model, the agents observe only the context distribution and the exact context is unknown to the agents. Such a situation arises, for instance, when the context itself is a noisy measurement or based on a prediction mechanism.
- Categories:
 25 Views
25 Views
- Read more about Importance Sampling Based Unsupervised Federated Representation Learning
- Log in to post comments
The use of AI has led to the era of pervasive intelligence, marked by a proliferation of smart devices in our daily lives. Federated Learning (FL) enables machine learning at the edge without having to share user-specific private data with an untrusted third party. Conventional FL techniques are supervised learning methods, where a fundamental challenge is to ensure that data is reliably annotated at the edge. Another approach is to obtain rich and informative representations ofunlabeled data, which is suitable for downstream tasks.
- Categories:
 24 Views
24 Views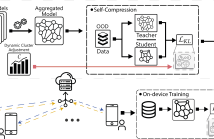
- Read more about Communication-Efficient Federated Learning through Adaptive Weight Clustering and Server-Side Distillation
- Log in to post comments
Federated Learning (FL) is a promising technique for the collaborative training of deep neural networks across multiple devices while preserving data privacy. Despite its potential benefits, FL is hindered by excessive communication costs due to repeated server-client communication during training.
2401.14211.pdf
- Categories:
 22 Views
22 Views
Federated learning is a technique that allows multiple entities to collaboratively train models using their data without compromising data privacy. However, despite its advantages, federated learning can be susceptible to false data injection attacks. In these scenarios, a malicious entity with control over specific agents in the network can manipulate the learning process, leading to a suboptimal model. Consequently, addressing these data injection attacks presents a significant research challenge in federated learning systems.
- Categories:
 16 Views
16 Views
- Read more about Towards Building the Federated GPT: Federated Instruction Tuning
- Log in to post comments
While "instruction-tuned" generative large language models (LLMs) have demonstrated an impressive ability to generalize to new tasks, the training phases heavily rely on large amounts of diverse and high-quality instruction data (such as ChatGPT and GPT-4). Unfortunately, acquiring high-quality instructions, especially when it comes to human-written instructions, can pose significant challenges both in terms of cost and accessibility. Moreover, concerns related to privacy can further limit access to such data, making the process of obtaining it a complex and nuanced undertaking.
- Categories:
 56 Views
56 Views
- Read more about META-KNOWLEDGE ENHANCED DATA AUGMENTATION FOR FEDERATED PERSON RE-IDENTIFICATION
- Log in to post comments
Recently, federated learning has been introduced into person re-identification (Re-ID) to avoid personal image leakage in traditional centralized training. To address the key issue of statistic heterogeneity in different clients, several optimization methods have been proposed to alleviate the bias of the local models. However, besides statistic heterogeneity, feature heterogeneity (e.g., various angles, different illuminations) in different clients is more challenging in federated Re-ID.
- Categories:
 17 Views
17 Views
- Read more about InfoShape: Task-Based Neural Data Shaping via Mutual Information
- Log in to post comments
The use of mutual information as a tool in private data sharing has remained an open challenge due to the difficulty of its estimation in practice. In this paper, we propose InfoShape, a task-based encoder that aims to remove unnecessary sensitive information from training data while maintaining enough relevant information for a particular ML training task. We achieve this goal by utilizing mutual information estimators that are based on neural networks, in order to measure two performance metrics, privacy and utility.
- Categories:
 10 Views
10 Views
- Read more about A Method to Reveal Speaker Identity in Distributed ASR Training, and How to Counter It
- Log in to post comments
End-to-end Automatic Speech Recognition (ASR) models are commonly trained over spoken utterances using optimization methods like Stochastic Gradient Descent (SGD). In distributed settings like Federated Learning, model training requires transmission of gradients over a network. In this work, we design the first method for revealing the identity of the speaker of a training utterance with access only to a gradient.
- Categories:
 24 Views
24 Views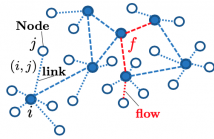
- Read more about Distributed Scheduling Using Graph Neural Networks
- Log in to post comments
A fundamental problem in the design of wireless networks is to efficiently schedule transmission in a distributed manner. The main challenge stems from the fact that optimal link scheduling involves solving a maximum weighted independent set (MWIS) problem, which is NP-hard. For practical link scheduling schemes, distributed greedy approaches are commonly used to approximate the solution of the MWIS problem. However, these greedy schemes mostly ignore important topological information of the wireless networks.
Zhao_ICASSP2021.pdf
- Categories:
 208 Views
208 Views
- Read more about Decentralized Optimization with Non-Identical Sampling in Presence of Stragglers
- Log in to post comments
We consider decentralized consensus optimization when workers sample data from non-identical distributions and perform variable amounts of work due to slow nodes known as stragglers. The problem of non-identical distributions and the problem of variable amount of work have been previously studied separately. In our work we analyse them together under a unified system model. We propose to combine worker outputs weighted by the amount of work completed by each.
- Categories:
 33 Views
33 Views