
- Categories:
 6 Views
6 Views
- Read more about Toeplitz Matrix Completion for Direction Finding Using a Modified Nested Linear Array
- Log in to post comments
A modified nested linear array (MNLA) has been reported recently for a greater potential in increasing the degree-of-freedom. However, there exist some “holes” in the difference co-array, which results in missing “lags” and limited performance of direction-of-arrival (DOA) estimation. In order to tackle this problem, this paper applies a Toeplitz matrix completion technique to MNLA, and investigates the performance of DOA estimation on this basis. Particularly, a semidefinite program with trace minimization is derived to obtain the covariance matrix with Hermitian and Toeplitz structure.
- Categories:
 60 Views
60 Views
In this paper, we are interested in the high-resolution
imaging of an unknown area based on only power measurements
of a small number of wireless transceivers located on one
side of the unknown area. In order to do so, we propose a
framework that achieves a polynomial order reduction in the
number of antennas required for high-resolution imaging. More
specifically, we show that by spacing the antennas at multiples
of the wavelength and applying subspace-based analysis, we can
image M targets using only 2M+1 transmit/receive antennas (as
- Categories:
 11 Views
11 Views
- Read more about Symmetric Sparse Linear Array for Active Imaging
- Log in to post comments
Sparse sensor arrays can achieve significantly more degrees of freedom than the number of elements by leveraging the co-array, a virtual structure that arises from the far field narrowband signal model. Although several sparse array configurations have been developed for passive sensing tasks, less attention has been paid to arrays suitable for active sensing. This paper presents a novel active sparse linear array, called the Interleaved Wichmann Array (IWA). The IWA only has a few closely spaced elements, which may make it more robust to mutual coupling effects.
sam_slides.pdf
- Categories:
 21 Views
21 Views
- Read more about Fast direction of arrival estimation using a sensor-saving coprime array with enlarged inter-element spacing
- Log in to post comments
- Categories:
 112 Views
112 Views
- Read more about EEG-Based Classification of Emotional State Using an Autonomous Vehicle Simulator
- Log in to post comments
Societal acceptance of self-driving cars (SDC) is predicated on a level of trust between humans and the au- tonomous vehicle. Although the performance of SDCs has im- proved dramatically, the question of mainstream acceptance and requisite trust is still open. We are exploring this question through integration of virtual reality SDC simulator and an electroencephalographic (EEG) recorder. In order for a passenger to build and maintain trust, the SDC will need to operate in a manner that elicits positive emotional response and avoids negative emotional response.
- Categories:
 44 Views
44 Views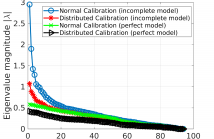
- Read more about Performance analysis of distributed radio interferometric calibration
- Log in to post comments
Distributed calibration based on consensus optimization is a computationally efficient method to calibrate large radio interferometers such as LOFAR and SKA. Calibrating along multiple directions in the sky and removing the bright foreground signal is a crucial step in many science cases in radio interferometry. The residual data contain weak signals of huge scientific interest and of particular concern is the effect of incomplete sky models used in calibration on the residual. In order to study this, we consider the mapping between the input uncalibrated data and the output residual data.
lofar75.pdf
lofar75.pdf
- Categories:
 6 Views
6 Views
- Read more about AN IMPROVED DOA ESTIMATOR BASED ON PARTIAL RELAXATION APPROACH
- Log in to post comments
In the partial relaxation approach, at each desired direction, the manifold structure of the remaining interfering signals impinging on the sensor array is relaxed, which results in closed form estimates for the interference parameters. By adopting this approach, in this paper, a new estimator based on the unconstrained covariance fitting problem is proposed. To obtain the null-spectra efficiently, an iterative rooting scheme based on the rational function approximation is applied.
- Categories:
 15 Views
15 Views
- Read more about Semidefinite Programming for TDOA Localization with Locally Synchronized Anchor Nodes
- Log in to post comments
The most state-of-art time-difference-of-arrival (TDOA) localization algorithms are performed under the assumption that all the nodes are synchronized. However, for a widely distributed wireless sensor networks (WSNs), time synchronization between all the nodes is not a trival problem. In this paper, we study the problem of source localization using signal TDOA measurements in the system of nodes part synchronization. Starting from the maximum likelihood estimator (MLE), we develop a semidefinite programming (SDP) approach.
- Categories:
 30 Views
30 Views