Sorry, you need to enable JavaScript to visit this website.

In the context of multivariate time series, a whiteness test against an MA(1)
correlation model is proposed. This test is built on the eigenvalue
distribution (spectral measure) of the non-Hermitian one-lag sample
autocovariance matrix, instead of its singular value distribution. The large
dimensional limit spectral measure of this matrix is derived. To obtain this
result, a control over the smallest singular value of a related random matrix
is provided. Numerical simulations show the excellent performance of this
test.

Conventional approaches to matrix completion are sensitive to outliers and impulsive noise. This paper develops robust and computationally efficient M-estimation based matrix completion algorithms. By appropriately arranging the observed entries, and then applying alternating minimization, the robust matrix completion problem is converted into a set of regression M-estimation problems. Making use of differ- entiable loss functions, the proposed algorithm overcomes a weakness of the lp-loss (p ≤ 1), which easily gets stuck in an inferior point.

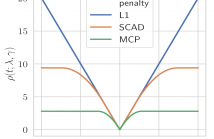
In this paper, we study the denoising of piecewise smooth graph sig-nals that exhibit inhomogeneous levels of smoothness over a graph. We extend the graph trend filtering framework to a family of non-convex regularizers that exhibit superior recovery performance overexisting convex ones. We present theoretical results in the form ofasymptotic error rates for both generic and specialized graph models. We further present an ADMM-based algorithm to solve the proposedoptimization problem and analyze its convergence.

Independent Vector Extraction aims at the joint blind source extraction of $K$ dependent signals of interest (SOI) from $K$ mixtures (one signal from one mixture). Similarly to Independent Component/Vector Analysis (ICA/IVA), the SOIs are assumed to be independent of the other signals in the mixture. Compared to IVA, the (de-)mixing IVE model is reduced in the number of parameters for the extraction problem. The SOIs are assumed to be non-Gaussian or noncircular Gaussian, while the other signals are modeled as circular Gaussian.

In this paper, we develop a novel method for approximate continuous-discrete Bayesian filtering. The projection filtering framework is exploited to develop accurate approximations of posterior distributions within parametric classes of probability distributions. This is done by formulating an ordinary differential equation for the posterior distribution that has the prior as initial value and hits the exact posterior after a unit of

Compressed sensing can be used to yield both compression and a limited form of security to the readings of sensors. This can be most useful when designing the low-resources sensor nodes that are the backbone of IoT applications. Here, we propose to use chaining of subsequent plaintexts to improve the robustness of CS-based encryption against ciphertext-only attacks, known-plaintext attacks and man-in-the-middle attacks.

In many signal processing tasks, one seeks to recover an r- column matrix object X ∈ Cn×r from a set of nonnegative quadratic measurements up to orthonormal transforms. Example applications include coherence retrieval in optical imaging and co- variance sketching for high-dimensional streaming data. To this end, efficient nonconvex optimization methods are quite appealing, due to their computational efficiency and scalability to large-scale problems.