
- Read more about Novel Bayesian Cluster Enumeration Criterion For Cluster Analysis With Finite Sample Penalty Term
- Log in to post comments
The Bayesian information criterion is generic in the sense that it does not include information about the specific model selection problem at hand. Nevertheless, it has been widely used to estimate the number of data clusters in cluster analysis. We have recently derived a Bayesian cluster enumeration criterion from first principles which maximizes the posterior probability of the candidate models given observations. But, in the finite sample regime, the asymptotic assumptions made by the criterion, to arrive at a computationally simple penalty term, are violated.
- Categories:
 9 Views
9 Views
- Read more about Novel Bayesian Cluster Enumeration Criterion For Cluster Analysis With Finite Sample Penalty Term
- Log in to post comments
The Bayesian information criterion is generic in the sense that it does not include information about the specific model selection problem at hand. Nevertheless, it has been widely used to estimate the number of data clusters in cluster analysis. We have recently derived a Bayesian cluster enumeration criterion from first principles which maximizes the posterior probability of the candidate models given observations. But, in the finite sample regime, the asymptotic assumptions made by the criterion, to arrive at a computationally simple penalty term, are violated.
- Categories:
 1 Views
1 Views
- Read more about Novel Bayesian Cluster Enumeration Criterion For Cluster Analysis With Finite Sample Penalty Term
- Log in to post comments
The Bayesian information criterion is generic in the sense that it does not include information about the specific model selection problem at hand. Nevertheless, it has been widely used to estimate the number of data clusters in cluster analysis. We have recently derived a Bayesian cluster enumeration criterion from first principles which maximizes the posterior probability of the candidate models given observations. But, in the finite sample regime, the asymptotic assumptions made by the criterion, to arrive at a computationally simple penalty term, are violated.
- Categories:
 2 Views
2 Views
- Read more about QUICKEST CHANGE-POINT DETECTION OVER MULTIPLE DATA STREAMS VIA SEQUENTIAL OBSERVATIONS
- Log in to post comments
- Categories:
 7 Views
7 Views
- Read more about Particle flow particle filter for Gaussian mixture noise models
- Log in to post comments
Particle filters has become a standard tool for state estimation in nonlinear systems. However, their performance usually deteriorates if the dimension of state space is high or the measurements are highly informative. A major challenge is to construct a proposal density that is well matched to the posterior distribution. Particle flow methods are a promising option for addressing this task. In this paper, we develop a particle flow particle filter algorithm to address the case where both the process noise and the measurement noise are distributed as mixtures of Gaussians.
- Categories:
 28 Views
28 Views
- Read more about Speaker Invariant Feature Extraction for Zero-Resource Languages with Adversarial Learning
- Log in to post comments
We introduce a novel type of representation learning to obtain a speaker invariant feature for zero-resource languages. Speaker adaptation is an important technique to build a robust acoustic model. For a zero-resource language, however, conventional model-dependent speaker adaptation methods such as constrained maximum likelihood linear regression are insufficient because the acoustic model of the target language is not accessible. Therefore, we introduce a model-independent feature extraction based on a neural network.
- Categories:
 22 Views
22 Views
- Read more about Efficient Estimation of Scatter Matrix with Convex Structure under t-distribution
- Log in to post comments
This paper addresses structured covariance matrix estimation under t-distribution. Covariance matrices frequently reveal a particular structure due to the considered application and taking into account this structure usually improves estimation accuracy. In the framework of robust estimation, the $t$-distribution is particularly suited to describe heavy-tailed observation. In this context, we propose an efficient estimation procedure for covariance matrices with convex structure under t-distribution.
- Categories:
 5 Views
5 Views
- Read more about OPTIMAL POOLING OF COVARIANCE MATRIX ESTIMATES ACROSS MULTIPLE CLASSES
- Log in to post comments
The paper considers the problem of estimating the covariance matrices of multiple classes in a low sample support condition, where the data dimensionality is comparable to, or larger than, the sample sizes of the available data sets. In such conditions, a common approach is to shrink the class sample covariance matrices (SCMs) towards the pooled SCM. The success of this approach hinges upon the ability to choose the optimal regularization parameter. Typically, a common regularization level is shared among the classes and determined via a procedure based on cross-validation.
- Categories:
 22 Views
22 Views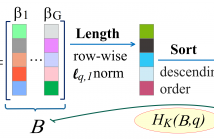
- Read more about Compressive Regularized Discriminant Analysis of High-Dimensional Data with Applications to Microarray Studies
- Log in to post comments
We propose a modification of linear discriminant analysis, referred to as compressive regularized discriminant analysis (CRDA), for analysis of high-dimensional datasets. CRDA is specially designed for feature elimination purpose and can be used as gene selection method in microarray studies. CRDA lends ideas from ℓq,1 norm minimization algorithms in the multiple measurement vectors (MMV) model and utilizes joint-sparsity promoting hard thresholding for feature elimination.
- Categories:
 13 Views
13 Views
- Read more about Change-Point Detection of Gaussian Graph Signals with Partial Information
- Log in to post comments
slides.pdf
- Categories:
 29 Views
29 Views