
- Read more about Slides: Change-Point Detection of Gaussian Graph Signals with Partial Information
- Log in to post comments
slides.pdf
- Categories:
 7 Views
7 Views
- Read more about Maximum-A-Posteriori Signal Recovery with Prior Information: Applications to Compressive Sensing
- Log in to post comments
- Categories:
 14 Views
14 Views
- Read more about 3D-HOG EMBEDDING FRAMEWORKS FOR SINGLE AND MULTI-VIEWPOINTS ACTION RECOGNITION BASED ON HUMAN SILHOUETTES
- Log in to post comments
Given the high demand for automated systems for human action recognition, great efforts have been undertaken in recent decades to progress the field. In this paper, we present frameworks for single and multi-viewpoints action recognition based on Space-Time Volume (STV) of human silhouettes and 3D-Histogram of Oriented Gradient (3D-HOG) embedding.
- Categories:
 13 Views
13 Views
- Read more about ROBUST SEQUENTIAL TESTING OF MULTIPLE HYPOTHESES IN DISTRIBUTED SENSOR NETWORKS
- Log in to post comments
The problem of sequential multiple hypothesis testing in a distributed sensor network is considered and two algorithms are proposed: the Consensus + Innovations Matrix Sequential Probability Ratio Test (CIMSPRT) for multiple simple hypotheses and the robust Least-Favorable-Density-CIMSPRT for hypotheses with uncertainties in the corresponding distributions. Simulations are performed to verify and evaluate the performance of both algorithms under different network conditions and noise contaminations.
- Categories:
 13 Views
13 Views- Read more about ON THE CONVERGENCE OF CONSTRAINED PARTICLE FILTERS
- Log in to post comments
The power of particle filters in tracking the state of non-linear and non-Gaussian systems stems not only from their simple numerical implementation but also from their optimality and convergence properties. In particle filtering, the posterior distribution of the state is approximated by a discrete mass of samples, called particles, that stochastically evolve in time according to the dynamics of the model and the observations. Particle filters have been shown to converge almost surely toward the optimal filter as the number of particles increases.
- Categories:
 29 Views
29 ViewsThe QR (Quick Response) code is a two-dimensional barcode, which was designed for storage information and high speed reading applications. Being cheap to produce and fast to read, it becomes actually a popular solution for product labeling.
Ones try to make QR code a solution against counterfeiting. We present a novel technique that permits to create a secure printed QR code which is robust
- Categories:
 768 Views
768 Views- Read more about COMPRESSIVE ONLINE ROBUST PRINCIPAL COMPONENT ANALYSIS WITH MULTIPLE PRIOR INFORMATION
- Log in to post comments
- Categories:
 9 Views
9 Views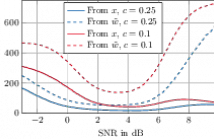
- Read more about Sequential Joint Signal Detection and Signal-to-Noise Ratio Estimation
- Log in to post comments
The sequential analysis of the problem of joint signal detection and signal-to-noise ratio (SNR) estimation for a linear Gaussian observation model is considered. The problem is posed as an optimization setup where the goal is to minimize the number of samples required to achieve the desired (i) type I and type II error probabilities and (ii) mean squared error performance.
- Categories:
 21 Views
21 Views
- Read more about Robust Particle Filter by Dynamic Averaging of Multiple Noise Models
- Log in to post comments
State filtering is a key problem in many signal processing applications. From a series of noisy measurement, one would like to estimate the state of some dynamic system. Existing techniques usually adopt a Gaussian noise assumption which may result in a major degradation in performance when the measurements are with the presence of outliers. A robust algorithm immune to the presence of outliers is desirable.
- Categories:
 8 Views
8 Views