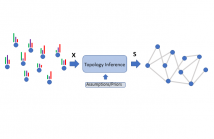
- Read more about Network Topology Inference from Gaussian and Stationary Graph Signals
- Log in to post comments
Graphs have become pervasive tools to represent information and datasets with irregular support. However, in many cases, the underlying graph is either unavailable or naively obtained, calling for more advanced methods for its estimation. Indeed, graph topology inference methods that estimate the network structure from a set of signal observations have a long and well-established history. By assuming that the observations are both Gaussian and stationary in the sought graph, this paper proposes a new scheme to learn the network from nodal observations.
- Categories:
 54 Views
54 Views
- Read more about COLUMN-BASED MATRIX APPROXIMATION WITH QUASI-POLYNOMIAL STRUCTURE
- Log in to post comments
A novel matrix completion problem is considered herein: observations based on fully sampled columns and quasi-polynomial side information is exploited. The framework is motivated by quantum chemistry problems wherein full matrix computation is expensive, but partial computations only lead to column information. The proposed algorithm successfully estimates the row-space of a true matrix given a priori knowledge of the true matrix. A theoretical error bound is provided, which captures the possible inaccuracies of the side information.
- Categories:
 23 Views
23 Views
- Read more about A Statistical Interpretation of the Maximum Subarray Problem
- Log in to post comments
Maximum subarray is a classical problem in computer science that given an array of numbers aims to find a contiguous subarray with the largest sum. We focus on its use for a noisy statistical problem of localizing an interval with a mean different from background. While a naive application of maximum subarray fails at this task, both a penalized and a constrained version can succeed.
Max_Subarray_video.pdf
- Categories:
 72 Views
72 Views
- Read more about Distributed Bayesian Tracking on the Special Euclidean Group using Lie Algebra Parametric Approximations
- Log in to post comments
This paper proposes new distributed particle filters for tracking the state of a dynamic system that evolves on the Special Euclidean Group. The algorithms are based on the Random Exchange diffusion technique and build compressed parametric approximations to the particles using Lie algebras. Via numerical simulations, we observe that the proposed methods perform similarly to a centralized particle filter, surpassing an extended Kalman filter by a large margin.
- Categories:
 20 Views
20 Views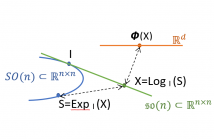
- Read more about Diffusion Particle Filtering on the Special Orthogonal Group Using Lie Algebra Statistics
- Log in to post comments
In this paper, we introduce new distributed diffusion algorithms to track a sequence of hidden random matrices that evolve on the special orthogonal group. The algorithms are based on the Adapt-then-Combine and the Random Exchange methods, and diffuse Gaussian approximations of posterior densities computed in the Lie algebra of the special orthogonal group. Simulation results show that, in scenarios with nonlinear observation functions, the proposed algorithms perform closely to the centralized particle filter estimator and can outperform competing Extended Kalman Filters.
spl_poster.pdf
- Categories:
 26 Views
26 Views
- Read more about DISTRIBUTED ONLINE LEARNING WITH ADVERSARIAL PARTICIPANTS IN AN ADVERSARIAL ENVIRONMENT
- Log in to post comments
This paper studies distributed online learning under Byzantine attacks. Performance of an online learning algorithm is characterized by (adversarial) regret, and a sublinear bound is preferred. But we prove that, even with a class of state-of-the-art robust aggregation rules, in an adversarial environment and with Byzantine participants, distributed online gradient descent can only achieve a linear adversarial regret bound, which is tight. This is the inevitable consequence
- Categories:
 12 Views
12 Views
- Read more about SPATIAL INFERENCE USING CENSORED MULTIPLE TESTING WITH FDR CONTROL
- Log in to post comments
A wireless sensor network performs spatial inference on a physical phenomenon of interest. The areas in which this phenomenon exhibits interesting or anomalous behavior are identified whilst controlling false positives. We expand our previous work based on multiple hypothesis testing (MHT) and local false discovery rates to save energy and reduce spectrum use. The number of transmissions from sensors producing uninformative statistics are reduced by introducing censoring for MHT that imposes a communication rate constraint while maintaining the desired performance.
- Categories:
 76 Views
76 Views
- Read more about High-Dimensional Sparse Bayesian Learning without Covariance Matrices
- Log in to post comments
- Categories:
 30 Views
30 Views
- Read more about Semi-supervised standardized detection of periodic signals with application to exoplanet detection
- Log in to post comments
We propose a numerical methodology for detecting periodicities in unknown colored noise and for evaluating the ‘significance levels’ (p-values) of the test statistics. The procedure assumes and leverages the existence of a set of time series obtained under the null hypothesis (a null training sample, NTS) and possibly complementary side information. The test statistic is computed from a standardized periodogram, which is a pointwise division of the periodogram of the series under test to an averaged periodogram obtained from the NTS.
- Categories:
 10 Views
10 Views
- Read more about A TEST FOR CONDITIONAL CORRELATION BETWEEN RANDOM VECTORS BASED ON WEIGHTED U-STATISTICS
- Log in to post comments
This article explores U-Statistics as a tool for testing conditional correlation between two multivariate sources with respect to a potential confounder. The proposed approach is effectively an instance of weighted U-Statistics and does not impose any statistical model on the processed data, in contrast to other well-known techniques that assume Gaussianity. By avoiding determinants and inverses, the method presented displays promising robustness in small-sample regimes. Its performance is evaluated numerically through its MSE and ROC curves.
- Categories:
 8 Views
8 Views