- Read more about Mobile Beamforming & Spatially Controlled Relay Communications
- Log in to post comments
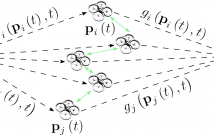
We consider stochastic motion planning in single-source single-destination robotic relay networks, under a cooperative beamforming framework. Assuming that the communication medium constitutes a spatiotemporal stochastic field, we propose a
- Categories:
 14 Views
14 Views- Read more about A SHORT-GRAPH FOURIER TRANSFORM VIA PERSONALIZED PAGERANK VECTORS
- Log in to post comments
The short-time Fourier transform (STFT) is widely used to analyze the spectra of temporal signals that vary through time. Signals defined over graphs, due to their intrinsic complexity, exhibit large variations in their patterns. In this work we propose a new formulation for an STFT for signals defined over graphs. This formulation draws on recent ideas from spectral graph theory, using personalized PageRank vectors as its fundamental building block.
poster.pdf
- Categories:
 19 Views
19 Views- Read more about EXTENSIONS OF SEMIDEFINITE PROGRAMMING METHODS FOR ATOMIC DECOMPOSITION
- Log in to post comments
We present an extension of recent semidefinite programming formulations for atomic decomposition over continuous dictionaries, with applications to continuous or 'gridless' compressed sensing. The dictionary considered in this paper is defined in terms of a general matrix pencil and is parameterized by a complex variable that varies over a segment of a line or circle in the complex plane. The main result of the paper is the formulation as a convex semidefinite optimization problem, and a simple constructive proof of the equivalence.
poster.pdf
- Categories:
 7 Views
7 Views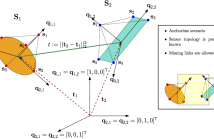
- Read more about Towards Multi-rigid Body Localization
- Log in to post comments
In this paper we focus on the relative position and orientation estimation between rigid bodies in an anchorless scenario. Several sensor units are installed on the rigid platforms, and the sensor placement on the rigid bodies is known beforehand (i.e., relative locations of the sensors on the rigid body are known). However, the absolute position of the rigid bodies is not known. We show that the relative localization of rigid bodies amounts to the estimation of a rotation matrix and the relative distance between the centroids of the rigid bodies.
- Categories:
 15 Views
15 Views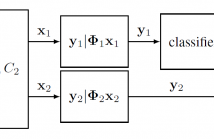
- Read more about A General Framework For Reconstruction and Classification From Compressive Measurements with Side Information
- Log in to post comments
poster.pdf
- Categories:
 14 Views
14 Views- Read more about COMMUTING OPERATOR OF OFFSET LINEAR CANONICAL TRANSFORM AND ITS APPLICATIONS
- Log in to post comments
Linear canonical transform (LCT) is an attractive and useful tool in optics and signal processing. In previous work, a generalization of the LCT with two extra parameters, called offset LCT (OLCT), has been developed. In this paper, a different definition of OLCT is proposed, which has a more concise form of inverse transform. We find a linear operator that commutes with the proposed OLCT. We prove that the commuting operator and the proposed OLCT have the same set of eigenfunctions with different eigenvalues.
- Categories:
 14 Views
14 Views- Read more about INDEPENDENT VERSUS REPEATED MEASUREMENTS: A PERFORMANCE QUANTIFICATION VIA STATE EVOLUTION
- Log in to post comments
The paper quantifies and compares the exact asymptotic performance of multiple measurement vector (MMV) and distributed sensing (DS) models. Both models assume multiple measurement instances y_k = A_kx_k + w_k; k = 1,2,...,K. The difference is that MMV involves identical measurement matrices whereas DS allows different matrices for different measurement instances. It has been recognized that DS works better than MMV empirically. However, the quantification of the performance difference is not available in the literature.
ICASSP2016.pdf
- Categories:
 15 Views
15 Views- Read more about ON ADAPTIVE SELECTION OF ESTIMATION BANDWIDTH FOR ANALYSIS OF LOCALLY STATIONARY MULTIVARIATE PROCESSES
- Log in to post comments
This is an overview poster on recent research of adaptive selection of estimation bandwidth for analysis of locally stationary multivariate processes.
- Categories:
 8 Views
8 Views- Read more about Physical modeling and performance bounds for device-free localization systems
- Log in to post comments
- Categories:
 5 Views
5 Views