Sorry, you need to enable JavaScript to visit this website.

Applications of signal processing and control are classically model-based, involving a two-step procedure for modeling and design: first a model is built from given data, and second, the estimated model is used for filtering, estimation, or control. Both steps typically involve optimization problems, but the combination of both is not necessarily optimal, and the modeling step often ignores the ultimate design objective. Recently, data-driven alternatives are receiving attention, which employ a direct approach combining the modeling and design into a single step.

The paper introduces a novel family of deterministic signals, the orthogonal periodic sequences (OPSs), for the identification of functional link polynomial (FLiP) filters. The novel sequences share many of the characteristics of the perfect periodic sequences (PPSs). As the PPSs, they allow the perfect identification of a FLiP filter on a finite time interval with the cross-correlation method. In contrast to the PPSs, OPSs can identify also non-orthogonal FLiP filters, as the Volterra filters.

In this paper, we address the fundamental problem of Sparse
Bayesian Learning (SBL), where the received signal is a high-order
tensor. We furthermore consider the problem of dictionary learning
(DL), where the tensor observations are assumed to be generated
from a Kronecker structured (KS) dictionary matrix multiplied by
the sparse coefficients. Exploiting the tensorial structure results in
a reduction in the number of degrees of freedom in the learning
problem, since the dimensions of each of the factor matrices are significantly

It is well known that empirical mode decomposition can suffer from computational instabilities at the signal boundaries. These ``end effects'' cause two problems: 1) sifting termination issues, i.e.~convergence and 2) estimation error, i.e.~accuracy. In this paper, we propose to use linear prediction in conjunction with a previous method to address end effects, to further mitigate these problems.

Without relative motion or beam scanning, orbitalangular-momentum (OAM)-based radar is shown to be able to estimate azimuth of targets, which opens a new perspective for traditional radar techniques. However, the existing application of two-dimensional (2-D) fast Fourier transform (FFT) and multiple signal classification (MUSIC) algorithms in OAM-based radar targets detection doesn’t realize 2-D super-resolution and robust estimation.

Graph convolutional networks adapt the architecture of convolutional neural networks to learn rich representations of data supported on arbitrary graphs by replacing the convolution operations of convolutional neural networks with graph-dependent linear operations. However, these graph-dependent linear operations are developed for scalar functions supported on undirected graphs. We propose both a generalization of the underlying graph and a class of linear operations for stochastic (time-varying) processes on directed (or undirected) graphs to be used in graph convolutional networks.

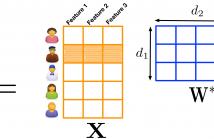
Inductive matrix completion (IMC) is a model for incorporating side information in form of “features” of the row and column entities of an unknown matrix in the matrix completion problem. As side information, features can substantially reduce the number of observed entries required for reconstructing an unknown matrix from its given entries. The IMC problem can be formulated as a low-rank matrix recovery problem where the observed entries are seen as measurements of a smaller matrix that models the interaction between the column and row features.