
- Read more about Conditional Density Driven Grid Design in Point-Mass Filter
- 1 comment
- Log in to post comments
- Categories:
 26 Views
26 Views
- Read more about PACO and PCO-DCT: Patch Consensus and Its Application To Inpainting
- Log in to post comments
Many signal processing methods break the target signal into overlapping patches, process them separately, and then stitch them back to produce an output. How to merge the resulting patches at the overlaps is central to such methods. We propose a novel framework for this type of problem based on the idea that estimated patches should coincide at the overlaps (consensus), and develop an algorithm for solving the general problem. In particular, an efficient method for projecting patches onto the consensus constraint is presented.
- Categories:
 22 Views
22 Views
- Read more about State-space Gaussian Process for Drift Estimation in Stochastic Differential Equations
- Log in to post comments
This paper is concerned with the estimation of unknown drift functions of stochastic differential equations (SDEs) from observations of their sample paths. We propose to formulate this as a non-parametric Gaussian process regression problem and use an Itô-Taylor expansion for approximating the SDE. To address the computational complexity problem of Gaussian process regression, we cast the model in an equivalent state-space representation, such that (non-linear) Kalman filters and smoothers can be used.
- Categories:
 17 Views
17 Views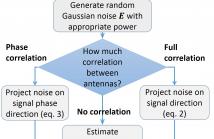
- Read more about Theoretical Performance Bound of Uplink Channel Estimation Accuracy in Massive MIMO
- Log in to post comments
In this paper, we present a new performance bound for uplink channel estimation (CE) accuracy in the Massive Multiple Input Multiple Output (MIMO) system. The proposed approach is based on noise power calculation after the CE unit in a multi-antenna receiver. Each time the impulse response of ideal channel estimation is decomposed into separate taps (beams) and cross-covariance matrix is calculated between them.
- Categories:
 25 Views
25 Views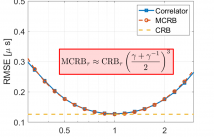
- Read more about Misspecified Cramer-Rao Bound For Delay Estimation With A Mismatched Waveform: A Case Study
- Log in to post comments
In this paper we investigate the problem of time of arrival estimation which occurs in many real-world applications, such as indoor localization or non-destructive testing via ultrasound or radar. A problem that is often overlooked when analyzing these systems is that in practice, we will typically not have exact information about the pulse shape. Therefore, there may be a mismatch between the parametric model that is assumed to derive and study the estimators versus the real model we find in practice.
- Categories:
 59 Views
59 Views
- Read more about EXTENDED CYCLIC COORDINATE DESCENT FOR ROBUST ROW-SPARSE SIGNAL RECONSTRUCTION IN THE PRESENCE OF OUTLIERS
- Log in to post comments
The problem of row-sparse signal reconstruction for complex-valued data with outliers is investigated in this paper. First, we formulate the problem by taking advantage of a sparse weight matrix, which is used to down-weight the outliers. The formulated problem belongs to LASSO-type problems, and such problems can be efficiently solved via cyclic coordinate descent (CCD). We propose an extended CCD algorithm to solve the problem for complex-valued measurements, which requires careful characterization and derivation.
- Categories:
 50 Views
50 Views
- Read more about Regularized partial phase synchrony index applied to dynamical functional connectivity estimation
- Log in to post comments
We study the inference of conditional independence graph from the partial Phase Locking Value (PLV) index of multivariate time series. A typical application is the inference of temporal functional connectivity from brain data. We extend the recently proposed time-varying graphical lasso to the measurement of partial locking values, yielding a sparse and temporally coherent dynamical graph that characterizes the evolution of the phase synchrony between each pair of signals.
PPFrusque.pdf
- Categories:
 17 Views
17 Views
- Read more about Estimating Centrality Blindly from Low-pass Filtered Graph Signals
- Log in to post comments
This work considers blind methods for centrality estimation from graph signals. We model graph signals as the outcome of an unknown
low-pass graph filter excited with influences governed by a sparse sub-graph. This model is compatible with a number of data
generation process on graphs, including stock data and opinion dynamics. Based on the said graph signal model, we first prove that the
- Categories:
 24 Views
24 Views
- Read more about Stability of Graph Neural Networks to Relative Perturbations
- Log in to post comments
Graph neural networks (GNNs), consisting of a cascade of layers applying a graph convolution followed by a pointwise nonlinearity, have become a powerful architecture to process signals supported on graphs. Graph convolutions (and thus, GNNs), rely heavily on knowledge of the graph for operation. However, in many practical cases the graph shift operator (GSO) is not known and needs to be estimated, or might change from training time to testing time.
- Categories:
 21 Views
21 Views