
- Read more about Denoising Deep Boltzmann Machines: Compression for Deep Learning
- Log in to post comments
- Categories:
 44 Views
44 Views
- Read more about $\alpha$ Belief Propagation as Fully Factorized Approximation
- Log in to post comments
poster.pdf
- Categories:
 24 Views
24 Views
- Read more about AMA: An Open-source Amplitude Modulation Analysis Toolkit for Signal Processing Applications
- Log in to post comments
For their analysis with conventional signal processing tools, non-stationary signals are assumed to be stationary (or at least wide-sense stationary) in short intervals. While this approach allows them to be studied, it disregards the temporal evolution of their statistics. As such, to analyze this type of signals, it is desirable to use a representation that registers and characterizes the temporal changes in the frequency content of the signals, as these changes may occur in single or multiple periodic ways.
globalsip_2019.pdf
- Categories:
 125 Views
125 Views
- Read more about On theoretical optimization of the sensing matrix for sparse-dictionary signal recovery
- Log in to post comments
Compressive Sensing (CS) is a new paradigm for the efficient acquisition of signals that have sparse representation in a certain domain. Traditionally, CS has provided numerous methods for signal recovery over an orthonormal basis. However, modern applications have sparked the emergence of related methods for signals not sparse in an orthonormal basis but in some arbitrary, perhaps highly overcomplete, dictionary, particularly due to their potential to generate different kinds of sparse representation of signals.
- Categories:
 177 Views
177 Views
Crowdsourcing platforms often want to incentivize workers to finish tasks with high quality and truthfully report their solutions. A high-quality solution requires a worker to exert effort; a platform can motivate such effort exertion and truthful reporting by providing a reward.
- Categories:
 52 Views
52 Views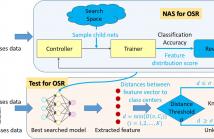
- Read more about Automatic neural network search method for Open Set Recognition
- Log in to post comments
Real-world recognition or classification tasks in computer vision are not apparent in controlled environments and often get involved in open set. Previous research work on real-world recognition problem is knowledge- and labor-intensive to pursue good performance for there are numbers of task domains. Auto Machine Learning (AutoML) approaches supply an easier way to apply advanced machine learning technologies, reduce the demand for experienced human experts and improve classification performance on close set.
- Categories:
 8 Views
8 Views
- Read more about A Characterization of Stochastic Mirror Descent Algorithms and Their Convergence Properties
- Log in to post comments
Stochastic mirror descent (SMD) algorithms have recently garnered a great deal of attention in optimization, signal processing, and machine learning. They are similar to stochastic gradient descent (SGD), in that they perform updates along the negative gradient of an instantaneous (or stochastically chosen) loss function. However, rather than update the parameter (or weight) vector directly, they update it in a "mirrored" domain whose transformation is given by the gradient of a strictly convex differentiable potential function.
- Categories:
 48 Views
48 Views
- Categories:
 25 Views
25 Views
- Read more about A DEEP NEURAL NETWORK BASED MANEUVERING-TARGET TRACKING ALGORITHM
- Log in to post comments
- Categories:
 20 Views
20 Views