- Read more about SAFE SCREENING FOR SPARSE REGRESSION WITH THE KULLBACK-LEIBLER DIVERGENCE
- Log in to post comments
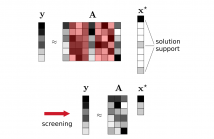
Safe screening rules are powerful tools to accelerate iterative solvers in sparse regression problems. They allow early identification of inactive coordinates (i.e., those not belonging to the support of the solution) which can thus be screened out in the course of iterations. In this paper, we extend the GAP Safe screening rule to the L1-regularized Kullback-Leibler divergence which does not fulfill the regularity assumptions made in previous works. The proposed approach is experimentally validated on synthetic and real count data sets.
- Categories:
 68 Views
68 Views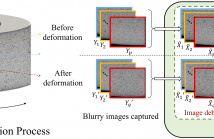
- Read more about FUSION-BASED DIGITAL IMAGE CORRELATION FRAMEWORKFOR STRAIN MEASUREMENT
- Log in to post comments
We address the problem of enabling two-dimensional digital image correlation (DIC) for strain measurement on large three-dimensional objects with curved surfaces. It is challenging to acquire full-field qualified images of the surface required by DIC due to geometric distortion and the narrow visual field of the surface that a single image can cover. To overcome this issue, we propose an end-to-end DIC framework incorporating the image fusion principle to achieve full-field strain measurement over the curved surface.
- Categories:
 27 Views
27 Views
- Read more about TIME-DOMAIN CONCENTRATION AND APPROXIMATION OF COMPUTABLE BANDLIMITED SIGNALS
- Log in to post comments
Turing computability deals with the question of what is theoretically computable on a digital computer, and hence is relevant whenever digital hardware is used. In this paper we study different possibilities to define computable bandlimited signals and systems. We consider a definition that uses finite Shannon sampling series as approximating functions and another that employs computable continuous functions together with an effectively computable time concentration. We discuss the advantages and drawbacks of both definitions and analyze the connections and differences.
- Categories:
 29 Views
29 Views
- Read more about Error estimate in second-order continuous-time sigma-delta modulators
- Log in to post comments
Continuous-time Sigma-Delta modulators are oversampling Analog-to-Digital converters that may provide higher sampling rates and lower power consumption than their discrete counterpart. Whereas approximation errors are established for high-order discrete time Sigma-Delta modulators, theoretical analysis of the error between the filtered output and the input remain scarce.
poster_1.pdf
- Categories:
 6 Views
6 Views
- Read more about Grid Optimization for Matrix-based Source Localization under Inhomogeneous Sensor Topology
- Log in to post comments
- Categories:
 3 Views
3 Views
- Read more about A Time-Based Sampling Framework for Finite-Rate-of-Innovation Signals
- Log in to post comments
Time-based sampling of continuous-time signals is an alternate sampling paradigm in which the signal is encoded using a sequence of non-uniform instants time. The standard methods for reconstructing bandlimited and shift-invariant signals from their time-encoded measurements employ alternating projections type methods. In this paper, we consider the problem of sampling and perfect reconstruction of periodic finite-rate-of-innovation (FRI) signals using crossing time-encoding machine (C-TEM) and integrate-and-fire TEM (IF-TEM).
- Categories:
 27 Views
27 Views
- Read more about Computing Hilbert Transform and Spectral Factorization for Signal Spaces of Smooth Functions
- Log in to post comments
Although the Hilbert transform and the spectral factorization are of central importance in signal processing,
- Categories:
 22 Views
22 Views
A Turing machine is a model describing the fundamental limits of any realizable computer, digital signal processor (DSP), or field programmable gate array (FPGA). This paper shows that there exist very simple linear time-invariant (LTI) systems which can not be simulated on a Turing machine. In particular, this paper considers the linear system described by the voltage-current relation of an ideal capacitor. For this system, it is shown that there exist continuously differentiable and computable input signals such that the output signal is a continuous function which is not computable.
- Categories:
 37 Views
37 Views
- Categories:
 12 Views
12 Views